Two constructions

In the past two weeks I posted on the arXiv two very different papers. One is in Discrete Geometry (joint with Karim Adiprasito) and another is in Asymptotic Group Theory (joint with Martin Kassabov). Both are fundamentally combinatorial, resolve (or at least advance) some rather old open problems, and leave some room for future work. And both are completely constructive, in a way a combinatorialist would appreciate.

If there is any moral of these two completely unrelated research projects, it’s that explicit combinatorial constructions are underrated and understudied. This is easy to explain. The elegance in structural results can be delightful and they bring order to a small part of the mathematical universe and can serve as a foundation for future work.

In contrast, new constructions create a mess that cannot be easily explained away and it can take time until they become accepted as a useful tool in the area. This phenomenon is similar to disproving famous conjectures that we talked about in this old blog post. Potentially, there are many more explicit combinatorial constructions both in positive and negative direction. All for the better, of course.

Stellar subdivisions

The paper All triangulations have a common stellar subdivision is available here (see also Karim’s blog post). The results are very general, but new already in the plane for triangulations of convex polygons. Let me state the main theorem in that case to give you a flavor what’s going on.

Let Q be a convex polygon in the plane. A triangulation of Q is a subdivision (face to face partition) of Q into triangles. For example, here is a triangulation of a triangle.

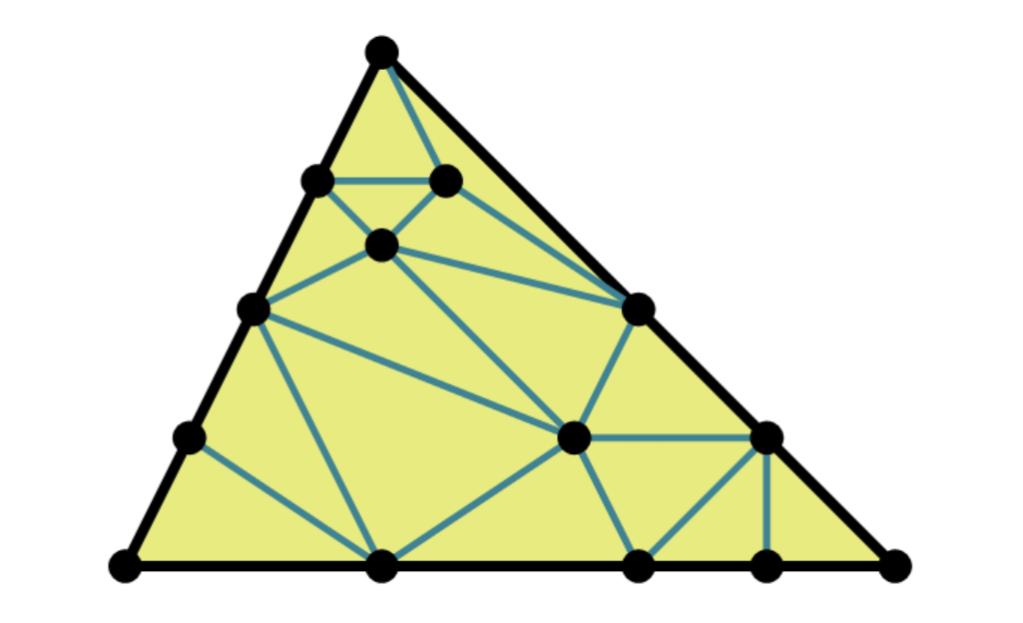
We now define stellar subdivisions as certain local transformations of triangulations. In the plane, there are two types: you can either place a new vertex inside the triangle and connect to vertices of the triangle, or you can place it on the edge and connect to vertices of triangles adjacent to this edge.

One can iterate such stellar subdivisions making triangulations more and more complicated, since at each step one new vertex is being added. If a triangulation C can be obtained from triangulations A and B by iterated stellar subdivisions, we say that A and B have a common subdivision C.

Theorem (Adiprasito-P.): Every two triangulations of a convex polygon in the plane have a common subdivision.

This may seem like a high school olympiad problem, and some day it probably will be. However, initially we thought this problem should have a negative answer. It was just too old and famous to have a positive solution, right? People must have tried everything, have they not? Well, I guess not.

In fact, it is well known and not very difficult to see that every two triangulations are connected by a sequence of stellar subdivisions and their inverses (in the plane, this was proved by Danilov in 1983, see refs in the paper). So the theorem really says that every two triangulations are connected by a sequence of stellar subdivisions followed by a sequence of inverse stellar subdivisions.

We give two closely related constructions in the paper: one that is more elementary and one that is less intuitive but is the starting point of a general construction (in a all dimensions). This resolves Oda’s (weighted) strong factorization conjecture. Another important consequence of our work is the proof of Alexander’s conjecture, which is essentially the same result but in topological setting.

The key open problem that’s left is the unweighted strong factorization conjecture, where the added points have additional constraints on their location (see Question 7.1 in the paper). It is unclear if one should believe in that conjecture at all, but our proof definitely breaks down.

Spectral radius

The paper Monotone parameters on Cayley graphs of finitely generated groups is available here. We obtain the main results about eight years ago, and only now got around to writing them. While writing, we generalized them to other what we call monotone parameters, but let me discuss only the spectral radius.

Let Γ=Cay(G,S) be a Cayley graph of an infinite group G with a symmetric generating set S. Let c(n) denote the number of words in S of length n equal to the identity e. Equivalently, c(n) is the number of loops in Γ of length n, starting and ending at e. The spectral radius ρ is defined as the limit

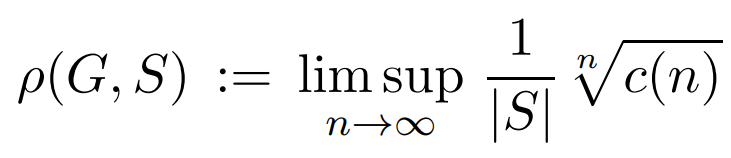
Famously, ρ=1 if an only if group G is amenable. There are several families of Cayley graphs where the spectral radius is known explicitly (free groups, free products of finite groups, etc.), but we really know very little:

Open Problem: What is the set X of all values of ρ over all pairs (G,S)? In particular, is X=(0,1]? If not, is X dense?

One version of the problem that I discuss in my ICM paper is this: Can one find an example of (G,S) such that ρ is transcendental? In this direction, Sarnak’s question (discussed e.g. here, Section G) asks whether the spectral radius for the surface group is transcendental? We give the following answer to the first question.

Theorem (Kassabov-P.) The set X of all spectral radii has cardinality of the continuum.

The result is proved by an explicit construction of a large family of 4-generated groups which gives an embedding of the Cantor set into X. Unfortunately, we are unable to give a single transcendental number which is a spectral radius of some group. One would think that there is some kind of Liouville number that comes out from the construction, and there surely is one, we just can’t give one explicitly.

The construction we give is based on another famous construction of the Grigorchuk group which disproved Milnor’s conjecture. This is a remarkable 4-generated group that has intermediate growth (both superpolynomial and subexponential). This group is the most famous example of a large uncountable family of such groups, and remains the source of many results and open problems.

While Grigorchuk’s groups are all amenable, of course, the flexibility of their structure allows one to decorate them. In our previous paper with Martin, we decorated them with finite expander quotients placed far apart to allow the oscillating intermediate growth. In this paper, we decorate them with nonamenable quotients to vary the spectral radii.

Of the many open problems that remain, let me single out one that is especially interesting from the computational combinatorics point of view. Recall that the Grigorchuk groups is not finitely presented, but is in fact recursively presented. Famously, it is not known whether there exist a finitely presented group of intermediate growth. Does there exists a finitely presented group with transcendental growth? Or at least recursively presented? We are nowhere close to resolving these questions.

UPDATE (Apr. 30, 2024). A finitely presented group with transcendental growth was just discovered by Corentin Bodart in this paper. Congratulations, Corentin!

The power of negative thinking: Combinatorial and geometric inequalities

It’s been awhile since I blogged about mathematics. You know why, of course — there are so many issues in the real world, the imaginary world is just not as relevant as it used to be. Well, at least that’s how I felt until now. But the latest paper we wrote with Swee Hong Chan was so much fun (and took so much effort), the wait is over. There is also some interesting backstory before we can state the result.

What is the inverse problem in Enumerative Combinatorics?

Before focusing on combinatorics, note that inverse problems are everywhere in mathematics. Sometimes they are obvious and stated as such, and sometimes we are so used to these problems we don’t think of them as inverse problems at all. You are probably thinking of major problems (both solved and unsolved), like the inverse Galois problem, Cauchy problem, Minkowski problem or the Alexandrov existence theorem. But really, even prime factorization, integration, taking logs and subtraction can be viewed this way. As I said — they are everywhere.

In Enumerative Combinatorics, a typical problem goes like this: given some set A, find the number N:=|A|. Finding a combinatorial interpretation is an inverse problem: given N, find A such that N=|A|. This might seem silly to an untrained eye: obviously, every nonnegative integer counts something. But it is completely normal to have constraints on the type of solution that you want — this case is no different.

Indeed, if you think about it, the direct problem is not all that well-defined either. For example, do you want an asymptotics or just some kind of bounds on N? Or maybe you want a closed formula? But what is a closed formula? Does it have to be a product formula, or some kind of summation will work? Can it be a multisum with both positive and negative terms? Or maybe you are ok with a closed formula for the generating function in case A=UA_n? But what exactly is a closed formula for a GF? The list of questions goes on.

Five years ago, I discussed various different answers to these question in my ICM paper, with ideas goes back to Wilf’s beautiful paper (see also Stanley’s answer). If anything, the answers are not short and sometimes technical. Although my formulations are well-defined, positive results can be hard to prove, while negative results can be really hard to prove. Such is life, I suppose.

So what exactly is a combinatorial interpretation?

It is easy to go philosophical (as Rota does or I do on somewhat broader questions), but let’s focus on math here. I started thinking about the problem when I came to UCLA over twelve years ago, and struggled to find a good answer. I discussed the problem in my Notices paper when I finally made peace with the computational complexity approach. Of the multiple definitions, there is only one that is both convincing, workable and broad enough:

Combinatorial interpretation = #P

I explain the answer in my lengthy OPAC survey on the subject, and in my somewhat entertaining OPAC talk (slides). I have miles to say about this, maybe some other time.

To understand why I case, it’s worth thinking of the origin of the problem. Say, you have an inequality a ≥ b between number of certain combinatorial objects, where a=|A|, b=|B|. If you have a nice explicit injection φ : B → A, this gives a combinatorial interpretation for the defect (a–b) as the number of elements in A without a preimage. If φ and its inverse are computable in polynomial time, this shows that (a–b) counts the number of objects which can be certified to be correct in polynomial time. Thus, the definition of #P.

Now, as always happens in these cases, the reason for the definition is not to give a positive answer (“you know it when you see it” was a guiding principle for a long time), but to give a negative answer. What if many of these combinatorial interpretation problems Stanley discusses in his famous survey simply don’t have a solution? (see my OPAC survey linked above, and this MO discussion for the state of art).

To list my favorite open problem, do Kronecker coefficients g(λ,μ,ν) have a combinatorial interpretation? I don’t believe so, but to give a negative answer we need a definition. There is just no way around it. Note that we already have g(λ,μ,ν)= a(λ,μ,ν) – b(λ,μ,ν) for some numbers of combinatorial objects a and b (formally, these are #P functions). It is the injection that doesn’t seem to work. But why not?

Unfortunately, the universe of “not in #P” results is very small and includes only this FOCS paper with Christian Ikenmeyer and this SODA paper with Christian Ikenmeyer and Greta Panova. Simply put, such results are rare and hard to prove. Let me not explain them, but rather turn in the direction of my current work.

Poset inequalities

Since the inequalities like g(λ,μ,ν) ≥ 0 are so unapproachable in full generality, some four years ago I turned to inequalities on the number of linear extensions of finite posets. Many such inequalities are known in the literature, e.g. the XYZ inequality, the Sidorenko inequality, the Björner–Wachs inequality, etc. It is unclear whether the defect of the XYZ inequality has a combinatorial interpretation, but the other two certainly do (see our “Effective poset inequalities” paper with Swee Hong Chan and Greta Panova).

What we found most interesting and challenging, is the following remarkable Stanley’s inequality on the log-concavity of the number of certain linear extensions:

(this is a slide from my 2021 talk). In a remarkable breakthrough, Stanley resolved the Chung-Fishburn-Graham conjecture using the Alexandrov–Fenchel inequality (more on this later). What I was interesting in the following problem: Is the defect of Stanley’s inequality N(k)^2-N(k-1) N(k+1) in #P? This is still an open problem, and we don’t have tools to resolve it.

It gets worse: in an effort to show that this inequality is in #P, two years ago we introduced a whole new technology of combinatorial atlas. We used this technology to prove a lot new inequalities in this paper with Swee Hong Chan, including multivariate extensions of Stanley inequalities and correlation inequalities. We now know why this technology was never going to apply to the #P problem, but that’s all yet another story.

What we did in our new paper is attacked a similar problem for the generalized Stanley inequality, which has the same statement but with additional constraints that L(x_i)=c_i for all 1 ≤ i ≤ m, where x_i are fixed poset elements and c_i are fixed integers. Stanley derived the log-concavity of these more general numbers from the AF inequality in one big swoosh. In our paper, we prove:

Corollary 1.5. The defect of the generalized Stanley inequality is not in #P, for all m ≥ 2 (unless PH collapses to a finite level).

Curiously, in addition to a lot of poset theoretic technology we are using the Yao-Knuth theorem in number theory. Our main result is stronger:

Theorem 1.3. The equality cases of the generalized Stanley inequality are not in PH, for all m ≥ 2 (unless PH collapses to a finite level).

Clearly, if the defect was in #P, then the “defect =^? 0″ is in coNP, and the “not in #P” result follows. The complexity theoretic idea of the proof is distilled in our companion paper where we explain why the coincidence problem for domino tilings in R³ is not in PH, and the same holds for many other hard combinatorial problems.

This underscores both the strength and the weakness of our approach. On the one hand, we prove a stronger result than we wanted. On the other hand, for m=0 it is known that the equality cases of the generalized Stanley inequality are in P. This is a remarkable result of Shenfeld and van Handel (actually, a consequence of the their remarkable theory). In fact, we reprove and generalize the result in our combinatorial atlas paper. In the new paper, we prove the m=1 version of this result, using a (also remarkable) followup paper by Ma and Shenfeld. We conjecture that m=2, the defect is already not in #P (Conjecture 10.2), but there seem to be difficult number theoretic obstacles to the proof.

In summary, we now know for sure that the defect of the generalized Stanley inequality does not have a combinatorial interpretation. In particular, there is no direct injective proof similar to that for the Sidorenko inequality, for example (cf. this old blog post). If you are deeply engaged with the subject (and why would you be, obviously?), you are happy. But if not — you probably shrug. Let me now explain why you should still care.

Geometric inequalities

It is rare when when you can honestly say this, but the geometric inequalities really do go back to antiquity (see e.g. here and there), when the isoperimetric inequality in the plane was first discovered. Of the numerous inequalities that followed, note the Brunn–Minkowski inequality and the Minkowski quadratic inequality (MQI) for three convex bodies in R³. These are all consequences of the Alexandrov–Fenchel inequality mentioned above. However, when it comes to equality conditions there is a bit of wrinkle.

For the isoperimetric inequality in the plane, the equality cases are obvious (discs), and there is an interesting history of proofs by symmetrization. For the BM inequality, the equality cases are homothetic convex bodies, but the proof is very far from obvious and requires the mixed volume machinery. For the MQI, the equality conditions were know only in some special cases, and resolved in full generality only recently by Shenfeld and van Handel.

For the AF inequality, the effort to understand the equality conditions goes back to A. D. Alexandrov, who found equality conditions in some cases:

Serious difficulties occur in determining the conditions for equality to hold in the general inequalities just derived. [Alexandrov, 1937]

In 1985, Rolf Schneider formulated a workable conjecture on the equality conditions, which remains out of reach in full generality. He made a strong case for the importance of the problem:

As [AF inequality] represents a classical inequality of fundamental importance and with many applications, the identification of the equality cases is a problem of intrinsic geometric interest. Without its solution, the Brunn–Minkowski theory of mixed volumes remains in an uncompleted state. [Schneider, 1994]

In the remarkable paper mentioned above, Shenfeld and van Handel resolved several special cases of the conjecture. Notably, they gave a complete characterization of the equality conditions for convex polytopes, in a sense of extracting all geometry from the problem, and stating the condition in terms of equality of certain mixed volumes. This is where we come in.

Equality cases of the AF inequality are not in PH

To understand the way Stanley derived his inequality from the AF inequality, it’s worth first explaining the connection to log-concavity:

Stanley considered sections P, Q of the order polytope associated with a given poset and concluded log-concavity for the numbers N(k) via a simple calculation.

Now, our “not in PH” theorem on the equality cases of Stanley’s inequality and this Stanley’s calculation imply that equality cases of the AF inequality are also not in PH (under the same complexity assumptions plus computational setup on how the polytopes are presented). In some sense, this says that the equality cases of the AF inequality can never be fully described, or at least the description by Shenfeld and van Handel is probably the best one can do.

In the spirit of the #P application, our result also implies, that there is unlikely to be a stability result for the AF inequality in full generality (in this sense), see Corollary 1.2 in the paper. Omitting precise statements and technicalities, let us only mention that Bonnesen’s inequality is a basic stability result which can be viewed as a sharp extension of the isoperimetric inequality, including the equality conditions. What we are saying is — don’t expect to ever see anything like that for the AF inequality (see the paper for details).

UPDATE (Feb. 7, 2024). The “m ≥ 6” was later improved to “m ≥ 2“, see our paper on the arXiv. See this video of my Oberwolfach talk on the subject. See also this blog post by Gil Kalai. Note: This paper was accepted to appear at STOC 2024. 

The journal hall of shame

As you all know, my field is Combinatorics. I care about it. I blog about it endlessly. I want to see it blossom. I am happy to see it accepted by the broad mathematical community. It’s a joy to see it represented at (most) top universities and recognized with major awards. It’s all mostly good.

Of course, not everyone is on board. This is normal. Changing views is hard. Some people and institutions continue insisting that Combinatorics is mostly a trivial nonsense (or at least large parts of it). This is an old fight best not rehashed again.

What I thought I would do is highlight a few journals which are particularly hostile to Combinatorics. I also make some comments below.

Hall of shame

The list below is in alphabetical order and includes only general math journals.

(1) American Journal of Mathematics

The journal had a barely mediocre record of publishing in Combinatorics until 2008 (10 papers out of 6544, less than one per 12 years of existence, mostly in the years just before 2008). But then something snapped. Zero Combinatorics papers since 2009. What happened??

The journal keeps publishing in other areas, obviously. Since 2009 it published the total of 696 papers. And yet not a single Combinatorics paper was deemed good enough. Really? Some 10 years ago while writing this blog post I emailed the AJM Editor Christopher Sogge asking if the journal has a policy or an internal bias against the area. The editorial coordinator replied:

I spoke to an editor: the AJM does not have any bias against combinatorics.  [2013]

You could’ve fooled me… Maybe start by admitting you have a problem.

(2) Cambridge Journal of Mathematics

This is a relative newcomer, established just ten years ago in 2013. CJM claims to:

publish papers of the highest quality, spanning the range of mathematics with an emphasis on pure mathematics.

Out of the 93 papers to date, it has published precisely Zero papers in Combinatorics. Yes, in Cambridge, MA which has the most active combinatorics seminar that I know (and used to co-organize twice a week). Perhaps, Combinatorics is not “pure” enough or simply lacks “papers of highest quality”.

Curiously, Jacob Fox is one of the seven “Associate Editors”. This makes me wonder about the CJM editorial policy, as in can any editor accept any paper they wish or the decision has to made by a majority of editors? Or, perhaps, each paper is accepted only by a unanimous vote? And how many Combinatorics papers were provisionally accepted only to be rejected by such a vote of the editorial board? Most likely, we will never know the answers…

(3) Compositio Mathematica

The journal also had a mediocre record in Combinatorics until 2006 (12 papers out of 2661). None among the last 1172 papers (since 2007). Oh, my… I wrote in this blog post that at least the journal is honest about Combinatorics being low priority. But I think it still has no excuse. Read the following sentence on their front page:

Papers on other topics are welcome if they are of broad interest.

So, what happened in 2007? Papers in Combinatorics suddenly lost broad interest? Quanta Magazine must be really confused by this all…

(4) Publications Mathématiques de l’IHÉS

Very selective. Naturally. Zero papers in Combinatorics. Yes, since 1959 they published the grand total of 528 papers. No Combinatorics papers made the cut. I had a very limited interaction with the journal when I submitted my paper which was rejected immediately. Here is what I got:

Unfortunately, the journal has such a severe backlog that we decided at the last meeting of the editorial board not to take any new submissions for the next few months, except possibly for the solution of a major open problem. Because of this I prefer to reject you paper right now. I am sorry that your paper arrived during that period. [2015]

I am guessing the editor (very far from my area) assumed that the open problem that I resolved in that paper could not possibly be “major” enough. Because it’s in Combinatorics, you see… But whatever, let’s get back to ZERO. Really? In the past 50 years Paris has been a major research center in my area, one of the best places to do Enumerative, Asymptotics and Algebraic Combinatorics. And none of that work was deemed worthy by this venerable journal??

Note: I used this link for a quick guide to top journals. It’s biased, but really any other ranking would work just as well. I used the MathSciNet to determine whether papers are in Combinatorics (search for MSC Primary = 05)

How should we understand this?

It’s all about making an effort. Some leading general journals like Acta, Advances, Annals, Duke, Inventiones, JAMS, JEMS, Math. Ann., Math. Z., etc. found a way to attract and publish Combinatorics papers. Mind you they publish very few papers in the area, but whatever biases they have, they apparently want to make sure combinatorialists would consider sending their best work to these journals.

The four hall of shamers clearly found a way to repel papers in Combinatorics, whether by exhibiting an explicit bias, not having a combinatorialist on the editorial board, never encouraging best people in the area to submit, or using random people to give “quick opinions” on work far away from their area of expertise.

Most likely, there are several “grandfathered areas” in each journal, so with the enormous growth of submissions there is simply no room for other areas. Here is a breakdown of the top five areas in Publ. Math. IHES, helpfully compiled by ZbMATH (out of 528, remember?):

Of course, for the CJM, the whole “grandfathered areas” reasoning does not apply. Here is their breakdown of the top five areas (out of 93). See any similarities? Looks like this is a distribution of areas that the editors think are “very very important”:

When 2/3 of your papers are in just two areas, “spanning the range of mathematics” this journal is not. Of course, it really doesn’t matter how the four hall of shamers managed to achieve their perfect record for so many years — the results speak for themselves.

What should you do about it?

Not much, obviously, unless you are an editor in either of these four journals. Please don’t boycott them — it’s counterproductive and they are already boycotting you. If you work in Combinatorics, you should consider submitting your best work there, especially if you have tenure and have nothing to lose by waiting. This was the advice I gave vis-à-vie the Annals and it still applies.

But perhaps you can also shame these journals. This was also my advice on MDPI Mathematics. Here some strategy is useful, so perhaps do this. Any time you are asked for a referee report or for a quick opinion, ask the editor: Does your journal have a bias against Combinatorics? If they want your help they will say “No”. If you write a positive opinion or a report, follow up and ask if the paper is accepted. If they say “No”, ask if they still believe the journal has no bias. Aim to exhaust them!

More broadly, tell everyone you know that these four journals have an anti-Combinatorics bias. As I quoted before, Noga Alon thinks that “mathematics should be considered as one unit“. Well, as long as these journals don’t publish in Combinatorics, I will continue to disagree, and so should you. Finally, if you know someone on the editorial board of these four journals, please send them a link to this blog post and ask to write a comment. We can all use some explanation…

How to start a paper?

Starting a paper is easy. That is, if you don’t care for the marketing, don’t want to be memorable, and just want to get on with the story and quickly communicate what you have proved. Fair enough.

But that only works when your story is very simple, as in “here is a famous conjecture which we solve in this paper”. You are implicitly assuming that the story of the conjecture has been told elsewhere, perhaps many times, so that the reader is ready to see it finally resolved. But if your story is more complicated, this “get to the point” approach doesn’t really work (and yes, I argue in this blog post and this article there is always a story). Essentially you need to prepare the reader for what’s to come.

In my “How to write a clear math paper” (see also my blog post) I recommend writing the Foreword — a paragraph or two devoted to philosophy underlying your work or a high level explanation of the key idea in your paper before you proceed to state the main result:

Consider putting in the Foreword some highly literary description of what you are doing. If it’s beautiful or sufficiently memorable, it might be quoted in other papers, sometimes on a barely related subject, and bring some extra clicks to your work. Feel free to discuss the big picture, NSF project outline style, mention some motivational examples in other fields of study, general physical or philosophical principles underlying your work, etc. There is no other place in the paper to do this, and I doubt referees would object if you keep your Foreword under one page. For now such discussions are relegated to surveys and monographs, which is a shame since as a result some interesting perspectives of many people are missing.

Martin Krieger has a similar idea which he discusses at length in his 2018 AMS Notices article Don’t Just Begin with “Let A be an algebra…” This convinced me that I really should follow his (and my own) advice.

So recently I took a stock of my open opening lines (usually, joint with coauthors), and found a mixed bag. I decided to list some of them below for your amusement. I included only those which are less closely related to the subject matter of the article, so might appeal to broader audience. I am grateful to all my collaborators which supported or at least tolerated this practice.

Combinatorics matters

Combinatorics has always been a battleground of tools and ideas. That’s why it’s so hard to do, or even define.

Combinatorial inequalities (2019)

The subject of enumerative combinatorics is both classical and modern. It is classical, as the basic counting questions go back millennia; yet it is modern in the use of a large variety of the latest ideas and technical tools from across many areas of mathematics. The remarkable successes from the last few decades have been widely publicized; yet they come at a price, as one wonders if there is anything left to explore. In fact, are there enumerative problems that cannot be resolved with existing technology?

Complexity problems in enumerative combinatorics (2018), see also this blog post.

Combinatorial sequences have been studied for centuries, with results ranging from minute properties of individual sequences to broad results on large classes of sequences. Even just listing the tools and ideas can be exhausting, which range from algebraic to bijective, to probabilistic and number theoretic. The existing technology is so strong, it is rare for an open problem to remain unresolved for more than a few years, which makes the surviving conjectures all the more interesting and exciting.

Pattern avoidance is not P-recursive (2015), see also this blog post.

In Enumerative Combinatorics, the results are usually easy to state. Essentially, you are counting the number of certain combinatorial objects: exactly, asymptotically, bijectively or otherwise. Judging the importance of the results is also relatively easy: the more natural or interesting the objects are, and the stronger or more elegant is the final formula, the better. In fact, the story or the context behind the results is usually superfluous since they speak for themselves.

Hook inequalities (2020)

Proof deconstruction

There are two schools of thought on what to do when an interesting combinatorial inequality is established. The first approach would be to treat it as a tool to prove a desired result. The inequality can still be sharpened or generalized as needed, but this effort is aimed with applications as the goal and not about the inequality per se.

The second approach is to treat the inequality as a result of importance in its own right. The emphasis then shifts to finding the “right proof” in an attempt to understand, refine or generalize it. This is where the nature of the inequality intervenes — when both sides count combinatorial objects, the desire to relate these objects is overpowering.

Effective poset inequalities (2022)

There is more than one way to explain a miracle. First, one can show how it is made, a step-by-step guide to perform it. This is the most common yet the least satisfactory approach as it takes away the joy and gives you nothing in return. Second, one can investigate away every consequence and implication, showing that what appears to be miraculous is actually both reasonable and expected. This takes nothing away from the miracle except for its shining power, and puts it in the natural order of things. Finally, there is a way to place the apparent miracle as a part of the general scheme. Even, or especially, if this scheme is technical and unglamorous, the underlying pattern emerges with the utmost clarity.

Hook formulas for skew shapes IV (2021)

In Enumerative Combinatorics, when it comes to fundamental results, one proof is rarely enough, and one is often on the prowl for a better, more elegant or more direct proof. In fact, there is a wide belief in multitude of “proofs from the Book”, rather than a singular best approach. The reasons are both cultural and mathematical: different proofs elucidate different aspects of the underlying combinatorial objects and lead to different extensions and generalizations.

Hook formulas for skew shapes II (2017)

Hidden symmetries

The phrase “hidden symmetries” in the title refers to coincidences between the numbers of seemingly different (yet similar) sets of combinatorial objects. When such coincidences are discovered, they tend to be fascinating because they reflect underlying algebraic symmetries — even when the combinatorial objects themselves appear to possess no such symmetries.

It is always a relief to find a simple combinatorial explanation of hidden symmetries. A direct bijection is the most natural approach, even if sometimes such a bijection is both hard to find and to prove. Such a bijection restores order to a small corner of an otherwise disordered universe, suggesting we are on the right path in our understanding. It is also an opportunity to learn more about our combinatorial objects.

Bijecting hidden symmetries for skew staircase shapes (2021)

Hidden symmetries are pervasive across the natural sciences, but are always a delight whenever discovered. In Combinatorics, they are especially fascinating, as they point towards both advantages and limitations of the tools. Roughly speaking, a combinatorial approach strips away much of the structure, be it algebraic, geometric, etc., while allowing a direct investigation often resulting in an explicit resolution of a problem. But this process comes at a cost — when the underlying structure is lost, some symmetries become invisible, or “hidden”.

Occasionally this process runs in reverse. When a hidden symmetry is discovered for a well-known combinatorial structure, it is as surprising as it is puzzling, since this points to a rich structure which yet to be understood (sometimes uncovered many years later). This is the situation of this paper.

Hidden symmetries of weighted lozenge tilings (2020)

Problems in Combinatorics

How do you approach a massive open problem with countless cases to consider? You start from the beginning, of course, trying to resolve either the most natural, the most interesting or the simplest yet out of reach special cases. For example, when looking at the billions and billions of stars contemplating the immense challenge of celestial cartography, you start with the closest (Alpha Centauri and Barnard’s Star), the brightest (Sirius and Canopus), or the most useful (Polaris aka North Star), but not with the galaxy far, far away.

Durfee squares, symmetric partitions and bounds on Kronecker coefficients (2022)

Different fields have different goals and different open problems. Most of the time, fields peacefully coexist enriching each other and the rest of mathematics. But occasionally, a conjecture from one field arises to present a difficult challenge in another, thus exposing its technical strengths and weaknesses. The story of this paper is our effort in the face of one such challenge.

Kronecker products, characters, partitions, and the tensor square conjectures (2016)

It is always remarkable and even a little suspicious, when a nontrivial property can be proved for a large class of objects. Indeed, this says that the result is “global”, i.e. the property is a consequence of the underlying structure rather than individual objects. Such results are even more remarkable in combinatorics, where the structures are weak and the objects are plentiful. In fact, many reasonable conjectures in the area fail under experiments, while some are ruled out by theoretical considerations.

Log-concave poset inequalities (2021)

Sometimes a conjecture is more than a straightforward claim to be proved or disproved. A conjecture can also represent an invitation to understand a certain phenomenon, a challenge to be confirmed or refuted in every particular instance. Regardless of whether such a conjecture is true or false, the advances toward resolution can often reveal the underlying nature of the objects.

On the number of contingency tables and the independence heuristic (2022)

Combinatorial Interpretations

Finding a combinatorial interpretation is an everlasting problem in Combinatorics. Having combinatorial objects assigned to numbers brings them depth and structure, makes them alive, sheds light on them, and allows them to be studied in a way that would not be possible otherwise. Once combinatorial objects are found, they can be related to other objects via bijections, while the numbers’ positivity and asymptotics can then be analyzed.

What is in #P and what is not? (2022)

Traditionally, Combinatorics works with numbers. Not with structures, relations between the structures, or connections between the relations — just numbers. These numbers tend to be nonnegative integers, presented in the form of some exact formula or disguised as probability. More importantly, they always count the number of some combinatorial objects.

This approach, with its misleading simplicity, led to a long series of amazing discoveries, too long to be recounted here. It turns out that many interesting combinatorial objects satisfy some formal relationships allowing for their numbers to be analyzed. More impressively, the very same combinatorial objects appear in a number of applications across the sciences.

Now, as structures are added to Combinatorics, the nature of the numbers and our relationship to them changes. They no longer count something explicit or tangible, but rather something ephemeral or esoteric, which can only be understood by invoking further results in the area. Even when you think you are counting something combinatorial, it might take a theorem or a even the whole theory to realize that what you are counting is well defined.

This is especially true in Algebraic Combinatorics where the numbers can be, for example, dimensions of invariant spaces, weight multiplicities or Betti numbers. Clearly, all these numbers are nonnegative integers, but as defined they do not count anything per se, at least in the most obvious or natural way.

What is a combinatorial interpretation? (2022)

Covering all bases

It is a truth universally acknowledged, that a combinatorial theory is often judged not by its intrinsic beauty but by the examples and applications. Fair or not, this attitude is historically grounded and generally accepted. While eternally challenging, this helps to keep the area lively, widely accessible, and growing in unexpected directions.

Hook formulas for skew shapes III (2019)

In the past several decades, there has been an explosion in the number of connections and applications between Geometric and Enumerative Combinatorics. Among those, a number of new families of “combinatorial polytopes” were discovered, whose volume has a combinatorial significance. Still, whenever a new family of n-dimensional polytopes is discovered whose volume is a familiar integer sequence (up to scaling), it feels like a “minor miracle”, a familiar face in a crowd in a foreign country, a natural phenomenon in need of an explanation.

Triangulations of Cayley and Tutte polytopes (2013)

The problem of choosing one or few objects among the many has a long history and probably existed since the beginning of human era (e.g. “Choose twelve men from among the people” Joshua 4:2). Historically this choice was mostly rational and random choice was considered to be a bad solution. Times have changed, however. [..] In many cases random solution has become desirable, if not the only possibility. Which means that it’s about time we understand the nature of a random choice.

When and how n choose k (1996)

Books are ideas

In his famous 1906 “white suit” speech, Mark Twain recalled a meeting before the House of Lords committee, where he argued in favor of perpetual copyright. According to Twain, the chairman of the committee with “some resentment in his manner,” countered: “What is a book? A book is just built from base to roof on ideas, and there can be no property in it.”

Sidestepping the copyright issue, the unnamed chairman had a point. In the year 2021, in the middle of the pandemic, books are ideas. They come in a variety of electronic formats and sizes, they can be “borrowed” from the “cloud” for a limited time, and are more ephemeral than long lasting. Clinging to the bygone era of safety and stability, we just keep thinking of them as sturdy paper volumes.

When it comes to math books, the ideas are fundamental. Really, we judge them largely based on the ideas they present, and we are willing to sacrifice both time and effort to acquire these ideas. In fact, as a literary genre, math books get away with a slow uninventive style, dull technical presentation, anticlimactic ending, and no plot to speak of. The book under review is very different. [..]

See this books review and this blog post (2021).

Warning: This post is not meant to be a writing advice. The examples I give are merely for amusement purposes and definitely not be emulated. I am happy with some of these quotes and a bit ashamed of others. Upon reflection, the style is overly dramatic most likely because I am overcompensating for something. But hey — if you are still reading this you probably enjoyed it…

How I chose Enumerative Combinatorics

Apologies for not writing anything for awhile. After Feb 24, the math part of the “life and math” slogan lost a bit of relevance, while the actual events were stupefying to the point when I had nothing to say about the life part. Now that the shock subsided, let me break the silence by telling an old personal story which is neither relevant to anything happening right now nor a lesson to anyone. Sometimes a story is just a story…

My field

As the readers of this blog know, I am a Combinatorialist. Not a “proud one”. Just “a combinatorialist”. To paraphrase a military slogan “there are many fields like this one, but this one is mine”. While I’ve been defending my field for years, writing about its struggles, and often defining it, it’s not because this field is more important than others. Rather, because it’s so frequently misunderstood.

In fact, I have worked in other (mostly adjacent) fields, but that was usually because I was curious. Curious what’s going on in other areas, curious if they had tools to help me with my problems. Curious if they had problems that could use my tools. I would go to seminars in other fields, read papers, travel to conferences, make friends. Occasionally this strategy paid off and I would publish something in another field. Much more often nothing ever came out of that. It was fun regardless.

Anyway, I wanted to work in combinatorics for as long as I can remember, since I was about 15 or so. There is something inherently discrete about the way I see the world, so much that having additional structure is just obstructing the view. Here is how Gian-Carlo Rota famously put it:

Combinatorics is an honest subject. […] You either have the right number or you haven’t. You get the feeling that the result you have discovered is forever, because it’s concrete. [Los Alamos Science, 1985]

I agree. Also, I really like to count. When prompted, I always say “I work in Combinatorics” even if sometimes I really don’t. But in truth, the field is much too large and not unified, so when asked to be more specific (this rarely happens) I say “Enumerative Combinatorics“. What follows is a short story of how I made the choice.

Family vacation

When I was about 18, Andrey Zelevinsky (ז״ל) introduced me and Alex Postnikov to Israel Gelfand and asked what should we be reading if we want to do combinatorics. Unlike most leading mathematicians in Russia, Gelfand had a surprisingly positive view on the subject (see e.g. his quotes here). He suggested we both read Macdonald’s book, which was translated into Russian by Zelevinsky himself just a few years earlier. The book was extremely informative but dry as a fig and left little room for creativity. I read a large chunk of it and concluded that if this is what modern combinatorics looks like, I want to have nothing to do with it. Alex had a very different impression, I think.

Next year, my extended family decided to have a vacation on a Russian “river cruise”. I remember a small passenger boat which left Moscow river terminal, navigated a succession of small rivers until it reached Volga. From there, the boat had a smooth gliding all the way to the Caspian Sea. The vacation was about three weeks of a hot Summer torture with the only relief served by mouth-watering fresh watermelons.

What made it worse, there was absolutely nothing to see. Much of the way Volga is enormously wide, sometimes as wide as the English channel. Most of the time you couldn’t even see the river banks. The cities distinguished themselves only by an assortment of Lenin statues, but were unremarkable otherwise. Volgograd was an exception with its very impressive tallest statue in Europe, roughly as tall as the Statue of Liberty when combined with its pedestal. Impressive for sure, but not worth the trip. Long story short, the whole cruise vacation was dreadfully boring.

One good book can make a difference

While most of my relatives occupied themselves by reading crime novels or playing cards, I was reading a math book, the only book I brought with me. This was Stanley’s Enumerative Combinatorics (vol. 1) whose Russian translation came out just a few months earlier. So I read it cover-to-cover, but doing only the easiest exercises just to make sure I understand what’s going on. That book changed everything…

Midway through, when I was reading about linear extensions of posets in Ch. 3 with their obvious connections to standard Young tableaux and the hook-length formula (which I already knew by then), I had an idea. From Macdonald’s book, I remembered the q-analogue of #SYT via the “charge“, a statistics introduced by Lascoux and Schützenberger to give a combinatorial interpretation of Kostka polynomials, and which works even for skew Young diagram shapes. I figured that skew shapes are generic enough, and there should be a generalization of the charge to all posets. After several long days filled with some tedious calculations by hand, I came up with both the statement and the proof of the q-analogue of the number of linear extensions.

I wrote the proof neatly in my notebook with a clear intent to publish my “remarkable discovery”, and continued reading. In Ch. 4, all of a sudden, I read the “P-partition theory” that I just invented by myself. It came with various applications and connections to other problems, and was presented so well, much nicer than I would have!

After some extreme disappointment, I learned from the notes that the P-partition theory was a large portion of Stanley’s own Ph.D. thesis, which he wrote before I was born. For a few hours, I did nothing but meditate, staring at the vast water surrounding me and ignoring my relatives who couldn’t care less what I was doing anyway. I was trying to think if there is a lesson in this fiasco.

It pays to be positive and self-assure, I suppose, in a way that only a teenager can be. That day I concluded that I am clearly doing something right, definitely smarter than everyone else even if born a little too late. More importantly, I figured that Enumerative Combinatorics done “Stanley-style” is really the right area for me…

Epilogue

I stopped thinking that I am smarter than everyone else within weeks, as soon as I learned more math. I no longer believe I was born too late. I did end up doing a lot of Enumerative Combinatorics. Much later I became Richard Stanley’s postdoc for a short time and a colleague at MIT for a long time. Even now, I continue writing papers on the numbers of linear extensions and standard Young tableaux. Occasionally, I also discuss their q-analogues (like in my most recent paper). I still care and it’s still the right area for me…

Some years later I realized that historically, the “charge” and Stanley’s q-statistics were not independent in a sense that both are generalizations of the major index by Percy MacMahon. In his revision of vol. 1, Stanley moved the P-partition theory up to Ch. 3, where it belongs IMO. In 2001, he received the Steele’s Prize for Mathematical Exposition for the book that changed everything…

The problem with combinatorics textbooks

Every now and then I think about writing a graduate textbook in Combinatorics, based on some topics courses I have taught. I scan my extensive lecture notes, think about how much time it would take, and whether there is even a demand for this kind of effort. Five minutes later I would always remember that YOLO, deeply exhale and won’t think about it for a while.

What’s wrong with Combinatorics?

To illustrate the difficulty, let me begin with two quotes which contradict each other in the most illuminating way. First, from the Foreword by Richard Stanley on (his former student) Miklós Bóna’s “A Walk Through Combinatorics” textbook:

The subject of combinatorics is so vast that the author of a textbook faces a difficult decision as to what topics to include. There is no more-or-less canonical corpus as in such other subjects as number theory and complex variable theory. [here]

Second, from the Preface by Kyle Petersen (and Stanley’s academic descendant) in his elegant “Inquiry-Based Enumerative Combinatorics” textbook:

Combinatorics is a very broad subject, so the difficulty in writing about the subject is not what to include, but rather what to exclude. Which hundred problems should we choose? [here]

Now that this is all clear, you can probably insert your own joke about importance of teaching inclusion-exclusion. But I think the issue is a bit deeper than that.

I’ve been thinking about this when updating my “What is Combinatorics” quotation page (see also my old blog post on this). You can see a complete divergence of points of view on how to answer this question. Some make the definition or description to be very broad (sometimes even ridiculously broad), some relatively narrow, some are overly positive, while others are revoltingly negative. And some basically give up and say, in effect “it is what it is”. This may seem puzzling, but if you concentrate on the narrow definitions and ignore the rest, a picture emerges.

Clearly, these people are not talking about the same area. They are talking about sub-areas of Combinatorics that they know well, that they happen to learn or work on, and that they happen to like or dislike. Somebody made a choice what part of Combinatorics to teach them. They made a choice what further parts of Combinatorics to learn. These choices are increasingly country or culture dependent, and became formative in people’s mind. And they project their views of these parts of Combinatorics on the whole field.

So my point is — there is no right answer to “What is Combinatorics?“, in a sense that all these opinions are biased to some degree by personal education and experience. Combinatorics is just too broad of a category to describe. It’s a bit like asking “what is good food?” — the answers would be either broad and bland, or interesting but very culture-specific.

Courses and textbooks

How should one resolve the issue raised above? I think the answer is simple. Stop claiming that Combinatorics, or worse, Discrete Mathematics, is one subject. That’s not true and hasn’t been true for a while. I talked about this in my “Unity of Combinatorics” book review. Combinatorics is comprised of many sub-areas, see the Wikipedia article I discussed here (long ago). Just accept it.

As a consequence, you should never teach a “Combinatorics” course. Never! Especially to graduate students, but to undergraduates as well. Teach courses in any and all of these subjects: Enumerative Combinatorics, Graph Theory, Probabilistic Combinatorics, Discrete Geometry, Algebraic Combinatorics, Arithmetic Combinatorics, etc. Whether introductory or advanced versions of these courses, there is plenty of material for each such course.

Stop using these broad “a little bit about everything” combinatorics textbooks which also tend to be bulky, expensive and shallow. It just doesn’t make sense to teach both the five color theorem and the Catalan numbers (see also here) in the same course. In fact, this is a disservice to both the students and the area. Different students want to know about different aspects of Combinatorics. Thus, if you are teaching the same numbered undergraduate course every semester you can just split it into two or three, and fix different syllabi in advance. The students will sort themselves out and chose courses they are most interested in.

My own teaching

At UCLA, with the help of the Department, we split one Combinatorics course into two titled “Graph Theory” and “Enumerative Combinatorics”. They are broader, in fact, than the titles suggest — see Math 180 and Math 184 here. The former turned out to be quite a bit more popular among many applied math and non-math majors, especially those interested in CS, engineering, data science, etc., but also from social sciences. Math majors tend to know a lot of this material and flock to the latter course. I am not saying you should do the same — this is just an example of what can be done.

I remember going through a long list of undergraduate combinatorics textbooks a few years ago, and found surprisingly little choice for the enumerative/algebraic courses. Of the ones I liked, let me single out Bóna’s “Introduction to Enumerative and Analytic Combinatorics“ and Stanley’s “Algebraic Combinatorics“. We now use both at UCLA. There are also many good Graph Theory course textbooks of all levels, of course.

Similarly, for graduate courses, make sure you make the subject relatively narrow and clearly defined. Like a topics class, except accessible to beginning graduate students. Low entry barrier is an advantage Combinatorics has over other areas, so use it. To give examples from my own teaching, see unedited notes from my graduate courses:

Combinatorics of posets (Fall 2020)

Combinatorics and Probability on groups (Spring 2020)

Algebraic Combinatorics (Winter 2019)

Discrete and Polyhedral Geometry (Fall 2018) This is based on my book. See also videos of selected topics (in Russian).

Combinatorics of Integer Sequences (Fall 2016)

Combinatorics of Words (Fall 2014)

Tilings (Winter 2013, lecture-by-lecture refs only)

In summary

In my experience, the more specific you make the combinatorics course the more interesting it is to the students. Don’t be afraid that the course would appear be too narrow or too advanced. That’s a stigma from the past. You create a good course and the students will quickly figure it out. They do have their own FB and other chat groups, and spread the news much faster than you could imagine…

Unfortunately, there is often no good textbook to cover what you want. So you might have to work a little harder harder to scout the material from papers, monographs, etc. In the internet era this is easier than ever. In fact, many extensive lecture notes are already available on the web. Eventually, all the appropriate textbooks will be written. As I mentioned before, this is one of the very few silver linings of the pandemic…

P.S. (July 8, 2021) I should have mentioned that in addition to “a little bit about everything” textbooks, there are also “a lot about everything” doorstopper size volumes. I sort of don’t think of them as textbooks at all, more like mixtures of a reference guide, encyclopedia and teacher’s manual. Since even the thought of teaching from such books overwhelms the senses, I don’t expect them to be widely adopted.

Having said that, these voluminous textbooks can be incredibly valuable to both the students and the instructor as a source of interesting supplementary material. Let me single out an excellent recent “Combinatorial Mathematics” by Doug West written in the same clear and concise style as his earlier “Introduction to Graph Theory“. Priced modestly (for 991 pages), I recommend it as “further reading” for all combinatorics courses, even though I strongly disagree with the second sentence of the Preface, per my earlier blog post.

The Unity of Combinatorics

I just finished my very first book review for the Notices of the AMS. The authors are Ezra Brown and Richard Guy, and the book title is the same as the blog post. I had mixed feelings when I accepted the assignment to write this. I knew this would take a lot of work (I was wrong — it took a huge amount of work). But the reason I accepted is because I strongly suspected that there is no “unity of combinatorics”, so I wanted to be proved wrong. Here is how the book begins:

One reason why Combinatorics has been slow to become accepted as part of mainstream Mathematics is the common belief that it consists of a bag of isolated tricks, a number of areas: [very long list – IP] with little or no connection between them. We shall see that they have numerous threads weaving them together into a beautifully patterned tapestry.

Having read the book, I continue to maintain that there is no unity. The book review became a balancing act — how do you write a somewhat positive review if you don’t believe into the mission of the book? Here is the first paragraph of the portion of the review where I touch upon themes very familiar to readers of this blog:

As I see it, the whole idea of combinatorics as a “slow to become accepted” field feels like a throwback to the long forgotten era. This attitude was unfair but reasonably common back in 1970, outright insulting and relatively uncommon in 1995, and was utterly preposterous in 2020.

After a lengthy explanation I conclude:

To finish this line of thought, it gives me no pleasure to conclude that the case for the unity of combinatorics is too weak to be taken seriously. Perhaps, the unity of mathematics as a whole is an easier claim to establish, as evident from [Stanley’s] quotes. On the other hand, this lack of unity is not necessarily a bad thing, as we would be amiss without the rich diversity of cultures, languages, open problems, tools and applications of different areas.

Enjoy the full review! And please comment on the post with your own views on this alleged “unity”.

P.S. A large part of the book is freely downloadable. I made this website for the curious reader.

Remark (ADDED April 17, 2021)
Ezra “Bud” Brown gave a talk on the book illustrating many of the connections I discuss in the review. This was at a memorial conference celebrating Richard Guy’s legacy. I was not aware of the video until now. Watch the whole talk.

What math stories to tell and not to tell?

Storytelling can be surprisingly powerful. When a story is skillfully told, you get an almost magical feeling of being a part of it, making you care deeply about protagonists. Even if under ordinary circumstances you have zero empathy for the Civil War era outlaws or emperor penguins of Antarctica, you suddenly may find yourself engrossed with their fortune. This is a difficult skill to master, but the effects are visible even when used in earnest by the beginners.

Recently I started thinking about the kind of stories mathematicians should be telling. This was triggered by Angela Gibney‘s kind invitation to contribute an article on math writing to the Early Career Collection in the Notices of the AMS. So I looked at a few older articles and found them just wonderful. I am not the target audience for some of them, but I just kept reading them all one after another until I exhausted the whole collection.

My general advice — read the collection! Read a few pieces by some famous people or some people you know. If you like them, keep on reading. As I wrote in this blog post, you rarely get an insight into mathematician’s thinking unless they happen to write an autobiography or gave an interview. While this is more of a “how to” genre, most pieces are written in the first person narrative and do tell some interesting stories or have some curious points of view.

It is possible I am the last person to find out about the collection. I am not a member of the AMS, I don’t read the Notices, and it’s been a long time since anyone considered me “early career”. I found a few articles a little self-centered (but who am I to judge), and I would quibble with some advice (see below). But even those articles I found compelling and thought-provoking.

Having read the collection, I decided to write about mathematical storytelling. This is not something that comes naturally to most people in the field. Math stories (as opposed to stories about mathematicians) tend to be rather dry and unexciting, especially in the early years of studying. I will blog my own article some other time, but for now let me address the question in the title.

Stories to tell

With a few notable exceptions, just about all stories are worth telling. Whether in your autobiography or in your personal blog, as long as they are interesting to somebody — it’s all good. Given the lack of good stories, or any math stories really, it’s a good bet somebody will find your stories interesting. Let me expound on that.

Basically, anything personal works. To give examples from the collection, see e.g. stories by Mark Andrea de Cataldo, Alicia Prieto-Langarica, Terry Tao and John Urschel. Most autobiographies are written in this style, but a short blog post is also great. Overcoming an embarrassment caused by such public disclosure can be difficult, which makes it even more valuable to the readers.

Anything historical works, from full length monographs on history of math to short point of view pieces. Niche and off the beaten path stories are especially valuable. I personally like the classical History of Mathematical Notations by Florian Cajori, and Combinatorics: Ancient & Modern, a nice collection edited by Robin Wilson and John Watkins, with a several articles authored by names you will recognize. Note that an oral history can be also very valuable, see the kind of stories discussed by László Lovász and Endre Szemerédi mentioned in this blog post and Dynkin’s interviews I discussed here.

Anything juicy works. I mean, if you have a story of some famous mathematician doing something unusual (good or bad, or just plain weird), that attracts attention. This was the style of Steven Krantz’s two Math Apocryphia books, with many revealing and embarrassing anecdotes giving a sense of the bygone era.

Anything inspirational works. A beautiful example of this style is Francis Su’s Farewell Address as MAA President and part of his moving follow up book (the book has other interesting material as well). From the collection, let me single out Finding Your Reward by Skip Garibaldi which also aims to inspire. Yet another example is Bill Thurston‘s must read MO answer “What’s a mathematician to do?“

Any off the beaten path math style is great. Think of “The Strong Law of Small Numbers” by Richard Guy, or many conjectures Terry Tao discusses in his blog. Think of “Missed opportunities” by Freeman Dyson, “Tilings of space by knotted tiles” by Colin Adams, or “One sentence proof… ” by Don Zagier (see also a short discussion here) — these are all remarkable and memorable pieces of writing that don’t conform to the usual peer review paradigm.

Finally, anything philosophical or metamathematical finds an audience. I am thinking of “Is it plausible?” by Barry Mazur, “Theorems for a Price” by Doron Zeilberger, “You and Your Research” by Richard Hamming, “Mathematics as Metaphor” by Yuri Manin, or even “Prime Numbers and the Search for Extraterrestrial Intelligence” by Carl Pomerance. We are all in search of some kind of answers, I suppose, so reading others thinking aloud about these deep questions always helps.

Practice makes perfect

Before I move to the other side, here is a simple advice on how to write a good story. Write as much as possible! There is no way around this. Absolutely no substitute, really. I’ve given this advice plenty of times, and so have everyone else. Let me conclude by this quote by Don Knuth which is a bit similar to Robert Lazarsfeld‘s advice. It makes my point much better and with with more authority that I can ever provide:

Of equal importance to solving a problem is the communication of that solution to others. The best way to improve your writing skills is to practice, practice, practice.

Seize every opportunity to write mini-essays about the theoretical work you are doing. Compose a blog for your friends, or even for yourself. When you write programs, write literate programs.

One of the best strategies to follow while doing PhD research is to prepare weekly reports of exactly what you are doing. What questions did you pursue that week? What positive answers did you get? What negative answers did you get? What are the major stumbling blocks that seem to be present at the moment? What related work are you reading?

Donald Knuth – On Writing up Research (posted by Omer Reingold), Theory Dish, Feb 26, 2018

Don’t be a journalist

In this interesting article in the same collection, Jordan Ellenberg writes:

Why don’t journalists talk about math as it really is? Because they don’t know how it really is. We do. And if we want the public discourse about math to be richer, broader, and deeper, we need to tell our own stories.

He goes on to suggest that one should start writing a blog and then pitch some articles to real newspapers and news magazines. He gives his own bio as one example (among others) of pitching and publishing in mainstream publications such as Slate and the New York Times. Obviously, I agree with the first (blog) part (duh!), but I am rather negative on the second part. I know, I know, this sounds discouraging, but hear me out.

First, what Jordan is not telling you is how hard he had to work on his craft before getting to the point of being acceptable to the general audience. This started with him getting Summa Cum Laude A.B. degree from Harvard in both Math and English (if I recall correctly), and then publishing a well-received novel, all before starting his regular Slate column. Very few math people have this kind of background on which they can build popular appeal.

Second, this takes away jobs from real journalists. Like every highly competitive intellectual profession, journalism requires years of study and practice. It has its own principles and traditions, graduate schools, etc. Call it a chutzpah or a Dunning–Kruger effect, but just because you are excellent in harmonic analysis doesn’t mean you can do even a mediocre job as a writer. Again — some people can do both, but most cannot. If anything, I suspect a negative correlation between math and writing skills.

Here is another way to think about this. Most people do realize that they don’t need to email their pretty iPhone pictures of a Machu Picchu sunrise to be published by the National Geographic. Or that their cobbler family recipe maybe not exactly be what Gourmet Magazine is looking for. Why would you think that writing is much easier then?

Third, this cheapens our profession to some degree. You really don’t need a Ph.D. in algebraic number theory and two perfect scores at the IMO to write about Powerball or baseball. You need a M.S. in statistics and really good writing skills. There are plenty of media sites which do that now, such as 538. There is even the whole DDJ specialization with many practitioners and a handful of Pulitzer prizes. Using quantitative methods is now mainstream, so what exactly are you bringing to the table?

Fourth, it helps to be honest. Jordan writes: “Editors like an angle. If there’s a math angle to a story in the news, pitch it! As someone with a degree in math, you have something to offer that most writers don’t.” This is true in the rare instances when, say, a Fields medal in your area is awarded, or something like that. But if it’s in an area far away from yours, then, uhm, you got nothing over many thousands of other people.

Now, please don’t take this as “don’t comment on current affairs” advice. No, no — please do! Comment away on your blog or on your podcast. Just don’t take jobs away from journalists. Help them instead! Write them emails, correct their mistakes. Let them interview you as an “expert”, whatever. Part of the reason the math related articles are so poor is because of mathematicians’ apathy and frequent disdain to the media, not because we don’t write newspaper articles — it’s really not our job.

Let me conclude with an anecdote about me reaching out to a newspaper. Once upon a time, long ago, flights used to distribute real newspapers to the passengers. I was sitting in the back and got a Wall Street Journal which I read out of boredom during takeoff. There was an article discussing the EU expansion and the fact that by some EU rules, the headquarters need a translator from every language to every other language. The article predicted dark days ahead, since it’s basically impossible to find people who can translate some smaller languages, such as from Maltese to Lithuanian. The article provided a helpful graph showing the number of translators needed as a function of the number of countries and claimed the exponential growth.

I was not amused, cut out the article, and emailed the author upon arrival, saying that with all my authority as an assistant professor at MIT, I promise that n(n-1) grows polynomially, not exponentially. I got back a surprisingly apologetic reply. The author confessed he was a math major in college, but was using the word without thinking. I don’t know if WSJ ever published a correction, but I bet the author will not be using this word so casually anymore, and if he ever advanced to the editorial position will propagate this knowledge to others. So there — that’s my personal contribution to improving public discourse…

Don’t be an apologist

In another beautifully written article in the Early Career collection, Izzet Coskun gives “advice on how to communicate mathematics quickly in informal settings”. He writes:

Whether before a promotion committee, at a party where one might meet future politicians or future parents of future colleagues, in the elevator on the way up to tea, or in the dean’s office at a job interview, we often have the opportunity to explain our work to a general audience. The time we have is usually short [..] Our audience will not be familiar with our terminology. Communicating mathematics in such settings is challenging.

He then gives a lot of very useful practical advice on how to prepare to such “math under a minute” conversation, how to be engaging, accessible, etc. It’s an all around good advice. However, I disagree. Here is my simple advice: Don’t Do It! If it’s a dean and this is a job interview, feel free to use any math jargon you want — it’s not your fault your field is technical, and the dean of sciences is used to it anyway. Otherwise, just say NO.

It’s true that sometimes your audience is friendly and is sincere in their interest in your work. In that case no matter what you say will disappoint them. There is a really good chance they can’t understand a word of what you say. They just think they can, and you are about to disillusion them.

But more often than not, the audience is actually not friendly, as was the case of a party Izzet described in his article. Many people harbor either a low regard or an outright resentment towards math stemming from their school years or some kind of “life experience”. These folks simply want to reinforce their views, and no matter what you say that will be taken as “you see, math is both hard, boring and useless”.

One should not confuse the unfriendlies with stupid or uneducated people. On the contrary, a lot of educated people think this way. A prime example is Amy Wax with her inimitable quote:

If we got rid of ninety percent of the math Ph.D. programs, would we really be worse off in any material respect?  I think that’s a serious question.

I discussed this quote at length in this blog post. There, I tried to answer her question. But after a few back-and-force emails (which I didn’t make public), it became clear that she is completely uninterested in the actual learning of what math is and what it does. She just wants to have her own answer validated by some area practitioners. Oh, well…

So here is the real reason why I think answering such people is pointless. No matter what you say, you come across as an apologist for the field. If people really want to understand what math is for, there are plenty of sources. In fact, have several bookshelves with extremely well written book-length answers. But it’s not your job to educate them! Worse, it is completely unreasonable to expect you to answer in “under one minute”.

Think about reactions of people when they meet other professionals. Someone says “I develop new DNA based cancer treatments” or “I work on improving VLSI architecture”, or “I device new option pricing strategies”. Is there a follow up request to explain it in “under one minute”? Not really. Let me give you a multiple choice. Is that because people think that:

a) these professions are boring compared to math and they would rather hear about the latter?

b) they know exactly what these professionals do, but math is so darn mysterious?

c) they know these professions are technical and hard to understand, but even children can understand math, so how hard can that be?

d) these professions are clearly useful, but what do math people do — solve quadratic equations all day?

If you answered a) or b) you have more faith in humanity than I do. If you answered c) you never spoke to anyone about math at a party. So d) is the only acceptable answer, even if it’s an exaggeration. Some people (mostly under 7) think that I “add numbers all day”, some people (mostly in social sciences) think that I “take derivatives all day”, etc., you get the point. My advice — don’t correct them. This makes them unhappy. Doesn’t matter if they are 7 or 77 — when you correct them the unhappiness is real and visible…

So here is a summary of how I deal with such questions. If people ask what I do, I answer “I do math research and I teach“. If they ask what kind of research I say “advanced math“. If they ask for details I tell them “it’s complicated“. If they ask why, I tell them “because it takes many years of study to even understand the math lingo, so if I tell you what I do this sounds like I am speaking a foreign language“.

If they ask what are the applications of my research (and they always do), I tell them “teaching graduate classes“. If they ask for “practical” applications, whatever that means, I tell them “this puts money into my Wells Fargo account“. At this point they move on exhausted by the questions. On the one hand I didn’t lie except in the last answer. On the other — nobody cares if I even have a WF account (I don’t, but it’s none of their business either).

One can ask — why do I care so much? What’s so special about my work that I am so apprehensive? In truth, nothing really. There are other aspects of my identity I also find difficult discussing in public. The most relevant is “What is Combinatorics?” which for some reason is asked over and over as if there is a good answer (see this blog post for my own answer and this Wikipedia article I wrote). When I hear people explaining what it is, half the time it sounds like they are apologizing for something they didn’t do…

There are other questions relevant to my complex identity that I am completely uninterested in discussing. Like “What do you think of the Russian President?” or “Who is a Jew?“, or “Are you a Zionist?” It’s not that my answers are somehow novel, interesting or controversial (they are not). It’s more like I am afraid to hear responses from the people who asked me these questions. More often than not I find their answers unfortunate or plain offensive, and I would rather not know that.

Let me conclude on a positive note, by telling a party story of my own. Once, during hors d’oeuvres (remember those?), one lady, a well known LA lawyer, walked to me and said: “I hear you are a math professor at UCLA. This is so fascinating! Can you tell me what you do? Just WOW me!” I politely declined along the lines above. She insisted: “There has to be something that I can understand!” I relented: “Ok, there is one theorem I can tell you. In fact, this result landed me a tenure.” She was all ears.

I continued: “Do you know what’s a square-root-of-two?” She nodded. “Well, I proved that this number can never be a ratio of two integers, for example it’s not equal to 17/12 or anything like that.” “Oh, shut-the-F-up!” she exclaimed. “Are you serious? You can prove that?” — she was clearly suspicious. “Yes, I can“, I confirmed vigorously, “in fact, two Russian newspapers even printed headlines about that back a few years ago. We love math over there, you know.”

“But of course!“, she said, “American media never writes about math. It’s such a shame! That’s why I never heard of your work. My son is much too young for this, but I must tell my nieces — they love science!” I nodded approvingly. She drifted away very happy, holding a small plate of meat stuffed potato croquettes, enriched with this newly acquired knowledge. I do hope her nieces liked that theorem — it is cool indeed. And the proof is so super neat…

Just combinatorics matters

I would really like everyone to know that every time you say or write that something is “just combinatorics” somebody rolls his eyes.  Guess who?

Here is a short collection of “just combinatorics” quotes.  It’s a followup on my “What is Combinatorics?” quotes page inspired by the “What is Combinatorics?” blog post.

The power of negative thinking, part I. Pattern avoidance

In my latest paper with Scott Garrabrant we disprove the Noonan-Zeilberger Conjecture. Let me informally explain what we did and why people should try to disprove conjectures more often.  This post is the first in a series.  Part II will appear shortly.

What did we do?

Let F ⊂ S_k be a finite set of permutations and let C_n(F) denote the number of permutations σ ∈ S_n avoiding the set of patterns F. The Noonan-Zeilbeger conjecture (1996), states that the sequence {C_n(F)} is always P-recursive. We disprove this conjecture.  Roughly, we show that every Turing machine T can be simulated by a set of patterns F, so that the number a_n of paths of length n accepted by by T is equal to C_n(F) mod 2.  I am oversimplifying things quite a bit, but that’s the gist.

What is left is to show how to construct a machine T such that {a_n} is not equal (mod 2) to any P-recursive sequence.  We have done this in our previous paper, where give a negative answer to a question by Kontsevich.  There, we constructed a set of 19 generators of GL(4,Z), such that the probability of return sequence is not P-recursive.

When all things are put together, we obtain a set F of about 30,000 permutations in S₈₀ for which {C_n(F)} is non-P-recursive.  Yes, the construction is huge, but so what?  What’s a few thousand permutations between friends?  In fact, perhaps a single pattern (1324) is already non-P-recursive.  Let me explain the reasoning behind what we did and why our result is much stronger than it might seem.

Why we did what we did

First, a very brief history of the NZ-conjecture (see Kirtaev’s book for a comprehensive history of the subject and vast references).  Traditionally, pattern avoidance dealt with exact and asymptotic counting of pattern avoiding permutations for small sets of patterns.  The subject was initiated by MacMahon (1915) and Knuth (1968) who showed that we get Catalan numbers for patterns of length 3.  The resulting combinatorics is often so beautiful or at least plentiful, it’s hard to imagine how can it not be, thus the NZ-conjecture.  It was clearly very strong, but resisted all challenges until now.  Wilf reports that Richard Stanley disbelieved it (Richard confirmed this to me recently as well), but hundreds of papers seemed to confirm its validity in numerous special cases.

Curiously, the case of the (1324) pattern proved difficult early on.  It remains unresolved whether C_n(1324) is P-recursive or not.  This pattern broke Doron Zeilberger’s belief in the conjecture, and he proclaimed that it’s probably non-P-recursive and thus NZ-conjecture is probably false.  When I visited Doron last September he told me he no longer has strong belief in either direction and encouraged me to work on the problem.  I took a train back to Manhattan looking over New Jersey’s famously scenic Amtrack route.  Somewhere near Pulaski Skyway I called Scott to drop everything, that we should start working on this problem.

You see, when it comes to pattern avoidance, things move from best to good to bad to awful.  When they are bad, they are so bad, it can be really hard to prove that they are bad.  But why bother – we can try to figure out something awful.  The set of patterns that we constructed in our paper is so awful, that proving it is awful ain’t so bad.

Why is our result much stronger than it seems?

That’s because the proof extends to other results.  Essentially, we are saying that everything bad you can do with Turing machines, you can do with pattern avoidance (mod 2).  For example, why is (1324) so hard to analyze?  That’s because it’s even hard to compute both theoretically and experimentally – the existing algorithms are recursive and exponential in n.  Until our work, the existing hope for disproving the NZ-conjecture hinged on finding an appropriately bad set of patterns such that computing {C_n(F)} is easy.  Something like this sequence which has a nice recurrence, but is provably non-P-recursive.  Maybe.  But in our paper, we can do worse, a lot worse…

We can make a finite set of patterns F, such that computing {C_n(F) mod 2} is “provably” non-polynomial (Th 1.4).  Well, we use quotes because of the complexity theory assumptions we must have.  The conclusion is much stronger than non-P-recursiveness, since every P-recursive sequence has a trivial polynomial in n algorithm computing it.  But wait, it gets worse!

We prove that for two sets of patterns F and G, the problem “C_n(F) = C_n(G) mod 2 for all n” is undecidable (Th 1.3).  This is already a disaster, which takes time to sink in.  But then it gets even worse!  Take a look at our Corollary 8.1.  It says that there are two sets of patterns F and G, such that you can never prove nor disprove that C_n(F) = C_n(G) mod 2.  Now that’s what I call truly awful.

What gives?

Well, the original intuition behind the NZ-conjecture was clearly wrong.  Many nice examples is not a good enough evidence.  But the conjecture was so plausible!  Where did the intuition fail?  Well, I went to re-read Polya’s classic “Mathematics and Plausible Reasoning“, and it all seemed reasonable.  That is both Polya’s arguments and the NZ-conjecture (if you don’t feel like reading the whole book, at least read Barry Mazur’s interesting and short followup).

Now think about Polya’s arguments from the point of view of complexity and computability theory.  Again, it sounds very “plausible” that large enough sets of patterns behave badly.  Why wouldn’t they?  Well, it’s complicated.  Consider this example.  If someone asks you if every 3-connected planar cubic graph has a Hamiltonian cycle, this sounds plausible (this is Tait’s conjecture).  All small examples confirm this.  Planar cubic graphs do have very special structure.  But if you think about the fact that even for planar graphs, Hamiltonicity is NP-complete, it doesn’t sound plausible anymore.  The fact that Tutte found a counterexample is no longer surprising.  In fact, the decision problem was recently proved to be NP-complete in this case.  But then again, if you require 4-connectivity, then every planar graph has a Hamiltonian cycle.  Confused enough?

Back to the patterns.  Same story here.  When you look at many small cases, everything is P-recursive (or yet to be determined).  But compare this with Jacob Fox’s theorem that for a random single pattern π, the sequence {C_n(π)} grows much faster than originally expected (cf. Arratia’s Conjecture).  This suggests that small examples are not representative of complexity of the problem.  Time to think about disproving ALL conjectures based on that evidence.

If there is a moral in this story, it’s that what’s “plausible” is really hard to judge.  The more you know, the better you get.  Pay attention to small crumbs of evidence.  And think negative!

What’s wrong with being negative?

Well, conjectures tend to be optimistic – they are wishful thinking by definition.  Who would want to conjecture that for some large enough a,b,c and n, there exist a solution of aⁿ + bⁿ = cⁿ?  However, being so positive has a drawback – sometimes you get things badly wrong.  In fact, even polynomial Diophantine equations can be as complicated as one wishes.  Unfortunately, there is a strong bias in Mathematics against counterexamples.  For example, only two of the Clay Millennium Problems automatically pay $1 million for a counterexample.  That’s a pity.  I understand why they do this, just disagree with the reasoning.  If anything, we should encourage thinking in the direction where there is not enough research, not in the direction where people are already super motivated to resolve the problem.

In general, it is always a good idea to keep an open mind.  Forget all this “power of positive thinking“, it’s not for math.  If you think a conjecture might be false, ignore everybody and just go for disproof.  Even if it’s one of those famous unsolved conjectures in mathematics.   If you don’t end up disproving the conjecture, you might have a bit of trouble publishing computational evidence.  There are some journals who do that, but not that many.  Hopefully, this will change soon…

Happy ending

When we were working on our paper, I wrote to Doron Zeilberger if he ever offered a reward for the NZ-conjecture, and for the disproof or proof only?  He replied with an unusual award, for the proof and disproof in equal measure.  When we finished the paper I emailed to Doron.  And he paid.  Nice… 🙂