Two constructions

In the past two weeks I posted on the arXiv two very different papers. One is in Discrete Geometry (joint with Karim Adiprasito) and another is in Asymptotic Group Theory (joint with Martin Kassabov). Both are fundamentally combinatorial, resolve (or at least advance) some rather old open problems, and leave some room for future work. And both are completely constructive, in a way a combinatorialist would appreciate.

If there is any moral of these two completely unrelated research projects, it’s that explicit combinatorial constructions are underrated and understudied. This is easy to explain. The elegance in structural results can be delightful and they bring order to a small part of the mathematical universe and can serve as a foundation for future work.

In contrast, new constructions create a mess that cannot be easily explained away and it can take time until they become accepted as a useful tool in the area. This phenomenon is similar to disproving famous conjectures that we talked about in this old blog post. Potentially, there are many more explicit combinatorial constructions both in positive and negative direction. All for the better, of course.

Stellar subdivisions

The paper All triangulations have a common stellar subdivision is available here (see also Karim’s blog post). The results are very general, but new already in the plane for triangulations of convex polygons. Let me state the main theorem in that case to give you a flavor what’s going on.

Let Q be a convex polygon in the plane. A triangulation of Q is a subdivision (face to face partition) of Q into triangles. For example, here is a triangulation of a triangle.

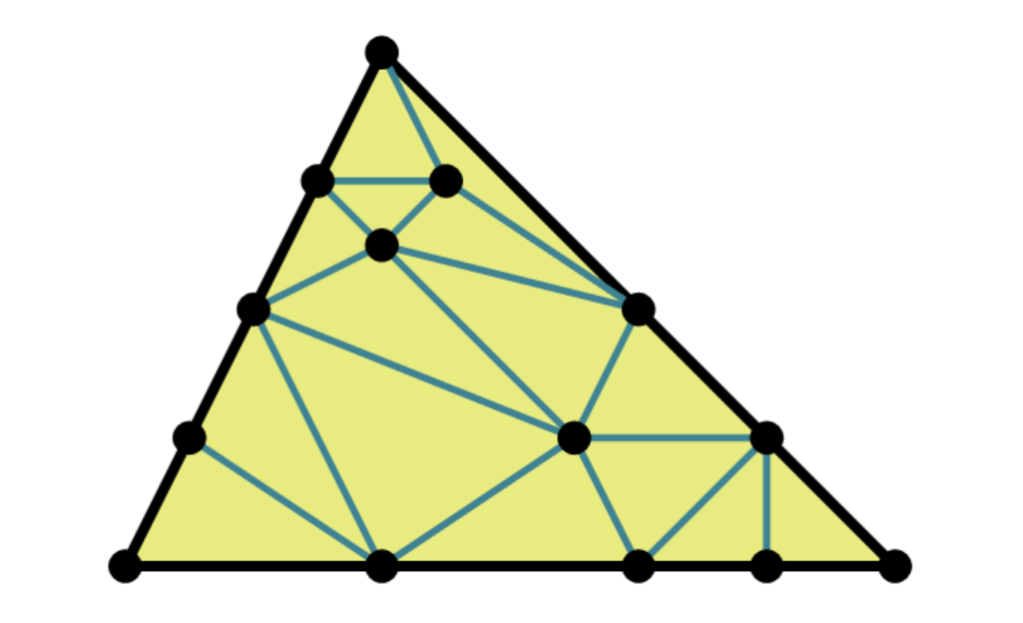
We now define stellar subdivisions as certain local transformations of triangulations. In the plane, there are two types: you can either place a new vertex inside the triangle and connect to vertices of the triangle, or you can place it on the edge and connect to vertices of triangles adjacent to this edge.

One can iterate such stellar subdivisions making triangulations more and more complicated, since at each step one new vertex is being added. If a triangulation C can be obtained from triangulations A and B by iterated stellar subdivisions, we say that A and B have a common subdivision C.

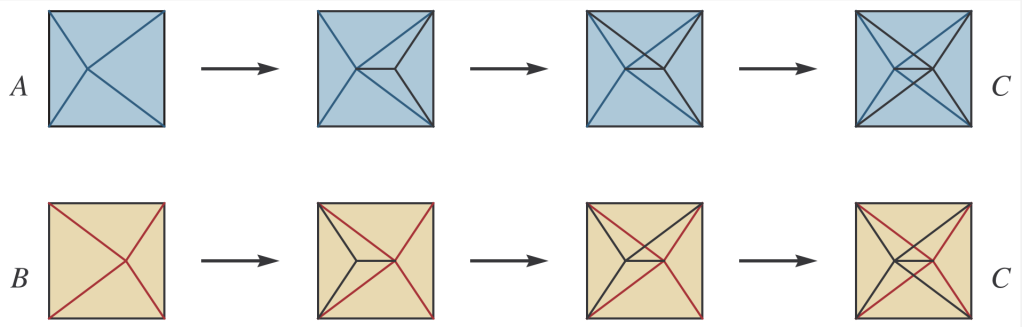
Theorem (Adiprasito-P.): Every two triangulations of a convex polygon in the plane have a common subdivision.

This may seem like a high school olympiad problem, and some day it probably will be. However, initially we thought this problem should have a negative answer. It was just too old and famous to have a positive solution, right? People must have tried everything, have they not? Well, I guess not.

In fact, it is well known and not very difficult to see that every two triangulations are connected by a sequence of stellar subdivisions and their inverses (in the plane, this was proved by Danilov in 1983, see refs in the paper). So the theorem really says that every two triangulations are connected by a sequence of stellar subdivisions followed by a sequence of inverse stellar subdivisions.

We give two closely related constructions in the paper: one that is more elementary and one that is less intuitive but is the starting point of a general construction (in a all dimensions). This resolves Oda’s (weighted) strong factorization conjecture. Another important consequence of our work is the proof of Alexander’s conjecture, which is essentially the same result but in topological setting.

The key open problem that’s left is the unweighted strong factorization conjecture, where the added points have additional constraints on their location (see Question 7.1 in the paper). It is unclear if one should believe in that conjecture at all, but our proof definitely breaks down.

Spectral radius

The paper Monotone parameters on Cayley graphs of finitely generated groups is available here. We obtain the main results about eight years ago, and only now got around to writing them. While writing, we generalized them to other what we call monotone parameters, but let me discuss only the spectral radius.

Let Γ=Cay(G,S) be a Cayley graph of an infinite group G with a symmetric generating set S. Let c(n) denote the number of words in S of length n equal to the identity e. Equivalently, c(n) is the number of loops in Γ of length n, starting and ending at e. The spectral radius ρ is defined as the limit

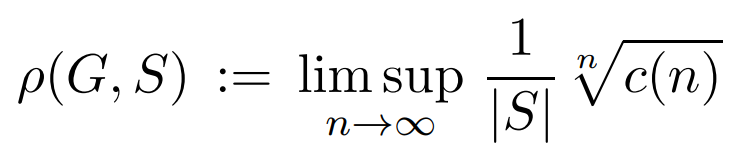
Famously, ρ=1 if an only if group G is amenable. There are several families of Cayley graphs where the spectral radius is known explicitly (free groups, free products of finite groups, etc.), but we really know very little:

Open Problem: What is the set X of all values of ρ over all pairs (G,S)? In particular, is X=(0,1]? If not, is X dense?

One version of the problem that I discuss in my ICM paper is this: Can one find an example of (G,S) such that ρ is transcendental? In this direction, Sarnak’s question (discussed e.g. here, Section G) asks whether the spectral radius for the surface group is transcendental? We give the following answer to the first question.

Theorem (Kassabov-P.) The set X of all spectral radii has cardinality of the continuum.

The result is proved by an explicit construction of a large family of 4-generated groups which gives an embedding of the Cantor set into X. Unfortunately, we are unable to give a single transcendental number which is a spectral radius of some group. One would think that there is some kind of Liouville number that comes out from the construction, and there surely is one, we just can’t give one explicitly.

The construction we give is based on another famous construction of the Grigorchuk group which disproved Milnor’s conjecture. This is a remarkable 4-generated group that has intermediate growth (both superpolynomial and subexponential). This group is the most famous example of a large uncountable family of such groups, and remains the source of many results and open problems.

While Grigorchuk’s groups are all amenable, of course, the flexibility of their structure allows one to decorate them. In our previous paper with Martin, we decorated them with finite expander quotients placed far apart to allow the oscillating intermediate growth. In this paper, we decorate them with nonamenable quotients to vary the spectral radii.

Of the many open problems that remain, let me single out one that is especially interesting from the computational combinatorics point of view. Recall that the Grigorchuk groups is not finitely presented, but is in fact recursively presented. Famously, it is not known whether there exist a finitely presented group of intermediate growth. Does there exists a finitely presented group with transcendental growth? Or at least recursively presented? We are nowhere close to resolving these questions.

UPDATE (Apr. 30, 2024). A finitely presented group with transcendental growth was just discovered by Corentin Bodart in this paper. Congratulations, Corentin!