Archive
The power of negative thinking: Combinatorial and geometric inequalities
It’s been awhile since I blogged about mathematics. You know why, of course — there are so many issues in the real world, the imaginary world is just not as relevant as it used to be. Well, at least that’s how I felt until now. But the latest paper we wrote with Swee Hong Chan was so much fun (and took so much effort), the wait is over. There is also some interesting backstory before we can state the result.
What is the inverse problem in Enumerative Combinatorics?
Before focusing on combinatorics, note that inverse problems are everywhere in mathematics. Sometimes they are obvious and stated as such, and sometimes we are so used to these problems we don’t think of them as inverse problems at all. You are probably thinking of major problems (both solved and unsolved), like the inverse Galois problem, Cauchy problem, Minkowski problem or the Alexandrov existence theorem. But really, even prime factorization, integration, taking logs and subtraction can be viewed this way. As I said — they are everywhere.
In Enumerative Combinatorics, a typical problem goes like this: given some set A, find the number N:=|A|. Finding a combinatorial interpretation is an inverse problem: given N, find A such that N=|A|. This might seem silly to an untrained eye: obviously, every nonnegative integer counts something. But it is completely normal to have constraints on the type of solution that you want — this case is no different.
Indeed, if you think about it, the direct problem is not all that well-defined either. For example, do you want an asymptotics or just some kind of bounds on N? Or maybe you want a closed formula? But what is a closed formula? Does it have to be a product formula, or some kind of summation will work? Can it be a multisum with both positive and negative terms? Or maybe you are ok with a closed formula for the generating function in case A=UAn? But what exactly is a closed formula for a GF? The list of questions goes on.
Five years ago, I discussed various different answers to these question in my ICM paper, with ideas goes back to Wilf’s beautiful paper (see also Stanley’s answer). If anything, the answers are not short and sometimes technical. Although my formulations are well-defined, positive results can be hard to prove, while negative results can be really hard to prove. Such is life, I suppose.
So what exactly is a combinatorial interpretation?
It is easy to go philosophical (as Rota does or I do on somewhat broader questions), but let’s focus on math here. I started thinking about the problem when I came to UCLA over twelve years ago, and struggled to find a good answer. I discussed the problem in my Notices paper when I finally made peace with the computational complexity approach. Of the multiple definitions, there is only one that is both convincing, workable and broad enough:
Combinatorial interpretation = #P
I explain the answer in my lengthy OPAC survey on the subject, and in my somewhat entertaining OPAC talk (slides). I have miles to say about this, maybe some other time.
To understand why I case, it’s worth thinking of the origin of the problem. Say, you have an inequality a ≥ b between number of certain combinatorial objects, where a=|A|, b=|B|. If you have a nice explicit injection φ : B → A, this gives a combinatorial interpretation for the defect (a–b) as the number of elements in A without a preimage. If φ and its inverse are computable in polynomial time, this shows that (a–b) counts the number of objects which can be certified to be correct in polynomial time. Thus, the definition of #P.
Now, as always happens in these cases, the reason for the definition is not to give a positive answer (“you know it when you see it” was a guiding principle for a long time), but to give a negative answer. What if many of these combinatorial interpretation problems Stanley discusses in his famous survey simply don’t have a solution? (see my OPAC survey linked above, and this MO discussion for the state of art).
To list my favorite open problem, do Kronecker coefficients g(λ,μ,ν) have a combinatorial interpretation? I don’t believe so, but to give a negative answer we need a definition. There is just no way around it. Note that we already have g(λ,μ,ν)= a(λ,μ,ν) – b(λ,μ,ν) for some numbers of combinatorial objects a and b (formally, these are #P functions). It is the injection that doesn’t seem to work. But why not?
Unfortunately, the universe of “not in #P” results is very small and includes only this FOCS paper with Christian Ikenmeyer and this SODA paper with Christian Ikenmeyer and Greta Panova. Simply put, such results are rare and hard to prove. Let me not explain them, but rather turn in the direction of my current work.
Poset inequalities
Since the inequalities like g(λ,μ,ν) ≥ 0 are so unapproachable in full generality, some four years ago I turned to inequalities on the number of linear extensions of finite posets. Many such inequalities are known in the literature, e.g. the XYZ inequality, the Sidorenko inequality, the Björner–Wachs inequality, etc. It is unclear whether the defect of the XYZ inequality has a combinatorial interpretation, but the other two certainly do (see our “Effective poset inequalities” paper with Swee Hong Chan and Greta Panova).
What we found most interesting and challenging, is the following remarkable Stanley’s inequality on the log-concavity of the number of certain linear extensions:
(this is a slide from my 2021 talk). In a remarkable breakthrough, Stanley resolved the Chung-Fishburn-Graham conjecture using the Alexandrov–Fenchel inequality (more on this later). What I was interesting in the following problem: Is the defect of Stanley’s inequality N(k)^2-N(k-1) N(k+1) in #P? This is still an open problem, and we don’t have tools to resolve it.
It gets worse: in an effort to show that this inequality is in #P, two years ago we introduced a whole new technology of combinatorial atlas. We used this technology to prove a lot new inequalities in this paper with Swee Hong Chan, including multivariate extensions of Stanley inequalities and correlation inequalities. We now know why this technology was never going to apply to the #P problem, but that’s all yet another story.
What we did in our new paper is attacked a similar problem for the generalized Stanley inequality, which has the same statement but with additional constraints that L(xi)=ci for all 1 ≤ i ≤ m, where xi are fixed poset elements and ci are fixed integers. Stanley derived the log-concavity of these more general numbers from the AF inequality in one big swoosh. In our paper, we prove:
Corollary 1.5. The defect of the generalized Stanley inequality is not in #P, for all m ≥ 2 (unless PH collapses to a finite level).
Curiously, in addition to a lot of poset theoretic technology we are using the Yao-Knuth theorem in number theory. Our main result is stronger:
Theorem 1.3. The equality cases of the generalized Stanley inequality are not in PH, for all m ≥ 2 (unless PH collapses to a finite level).
Clearly, if the defect was in #P, then the “defect =? 0″ is in coNP, and the “not in #P” result follows. The complexity theoretic idea of the proof is distilled in our companion paper where we explain why the coincidence problem for domino tilings in R3 is not in PH, and the same holds for many other hard combinatorial problems.
This underscores both the strength and the weakness of our approach. On the one hand, we prove a stronger result than we wanted. On the other hand, for m=0 it is known that the equality cases of the generalized Stanley inequality are in P. This is a remarkable result of Shenfeld and van Handel (actually, a consequence of the their remarkable theory). In fact, we reprove and generalize the result in our combinatorial atlas paper. In the new paper, we prove the m=1 version of this result, using a (also remarkable) followup paper by Ma and Shenfeld. We conjecture that m=2, the defect is already not in #P (Conjecture 10.2), but there seem to be difficult number theoretic obstacles to the proof.
In summary, we now know for sure that the defect of the generalized Stanley inequality does not have a combinatorial interpretation. In particular, there is no direct injective proof similar to that for the Sidorenko inequality, for example (cf. this old blog post). If you are deeply engaged with the subject (and why would you be, obviously?), you are happy. But if not — you probably shrug. Let me now explain why you should still care.
Geometric inequalities
It is rare when when you can honestly say this, but the geometric inequalities really do go back to antiquity (see e.g. here and there), when the isoperimetric inequality in the plane was first discovered. Of the numerous inequalities that followed, note the Brunn–Minkowski inequality and the Minkowski quadratic inequality (MQI) for three convex bodies in R3. These are all consequences of the Alexandrov–Fenchel inequality mentioned above. However, when it comes to equality conditions there is a bit of wrinkle.
For the isoperimetric inequality in the plane, the equality cases are obvious (discs), and there is an interesting history of proofs by symmetrization. For the BM inequality, the equality cases are homothetic convex bodies, but the proof is very far from obvious and requires the mixed volume machinery. For the MQI, the equality conditions were know only in some special cases, and resolved in full generality only recently by Shenfeld and van Handel.
For the AF inequality, the effort to understand the equality conditions goes back to A. D. Alexandrov, who found equality conditions in some cases:
Serious difficulties occur in determining the conditions for equality to hold in the general inequalities just derived. [Alexandrov, 1937]
In 1985, Rolf Schneider formulated a workable conjecture on the equality conditions, which remains out of reach in full generality. He made a strong case for the importance of the problem:
As [AF inequality] represents a classical inequality of fundamental importance and with many applications, the identification of the equality cases is a problem of intrinsic geometric interest. Without its solution, the Brunn–Minkowski theory of mixed volumes remains in an uncompleted state. [Schneider, 1994]
In the remarkable paper mentioned above, Shenfeld and van Handel resolved several special cases of the conjecture. Notably, they gave a complete characterization of the equality conditions for convex polytopes, in a sense of extracting all geometry from the problem, and stating the condition in terms of equality of certain mixed volumes. This is where we come in.
Equality cases of the AF inequality are not in PH
To understand the way Stanley derived his inequality from the AF inequality, it’s worth first explaining the connection to log-concavity:
Stanley considered sections P, Q of the order polytope associated with a given poset and concluded log-concavity for the numbers N(k) via a simple calculation.
Now, our “not in PH” theorem on the equality cases of Stanley’s inequality and this Stanley’s calculation imply that equality cases of the AF inequality are also not in PH (under the same complexity assumptions plus computational setup on how the polytopes are presented). In some sense, this says that the equality cases of the AF inequality can never be fully described, or at least the description by Shenfeld and van Handel is probably the best one can do.
In the spirit of the #P application, our result also implies, that there is unlikely to be a stability result for the AF inequality in full generality (in this sense), see Corollary 1.2 in the paper. Omitting precise statements and technicalities, let us only mention that Bonnesen’s inequality is a basic stability result which can be viewed as a sharp extension of the isoperimetric inequality, including the equality conditions. What we are saying is — don’t expect to ever see anything like that for the AF inequality (see the paper for details).
UPDATE (Feb. 7, 2024). The “m ≥ 6” was later improved to “m ≥ 2“, see our paper on the arXiv. See this video of my Oberwolfach talk on the subject. See also this blog post by Gil Kalai. Note: This paper was accepted to appear at STOC 2024.
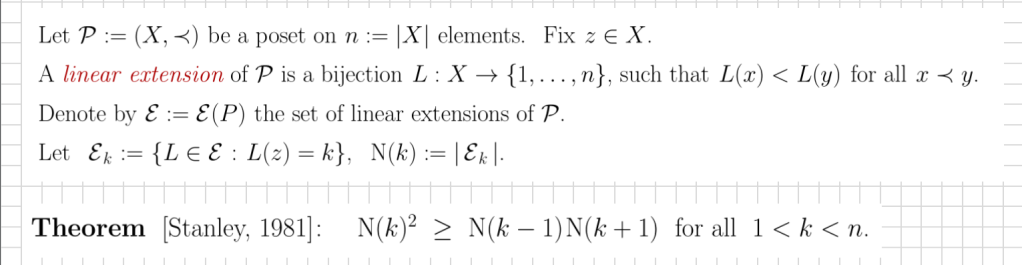
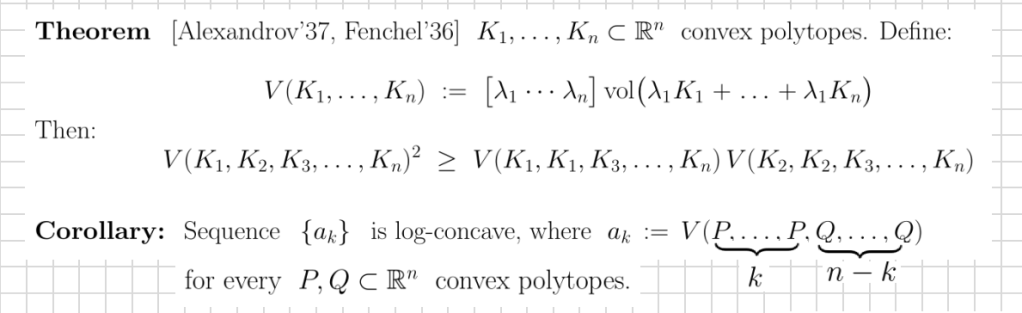
You must be logged in to post a comment.