Archive
The journal hall of shame
As you all know, my field is Combinatorics. I care about it. I blog about it endlessly. I want to see it blossom. I am happy to see it accepted by the broad mathematical community. It’s a joy to see it represented at (most) top universities and recognized with major awards. It’s all mostly good.
Of course, not everyone is on board. This is normal. Changing views is hard. Some people and institutions continue insisting that Combinatorics is mostly a trivial nonsense (or at least large parts of it). This is an old fight best not rehashed again.
What I thought I would do is highlight a few journals which are particularly hostile to Combinatorics. I also make some comments below.
Hall of shame
The list below is in alphabetical order and includes only general math journals.
(1) American Journal of Mathematics
The journal had a barely mediocre record of publishing in Combinatorics until 2008 (10 papers out of 6544, less than one per 12 years of existence, mostly in the years just before 2008). But then something snapped. Zero Combinatorics papers since 2009. What happened??
The journal keeps publishing in other areas, obviously. Since 2009 it published the total of 696 papers. And yet not a single Combinatorics paper was deemed good enough. Really? Some 10 years ago while writing this blog post I emailed the AJM Editor Christopher Sogge asking if the journal has a policy or an internal bias against the area. The editorial coordinator replied:
I spoke to an editor: the AJM does not have any bias against combinatorics. [2013]
You could’ve fooled me… Maybe start by admitting you have a problem.
(2) Cambridge Journal of Mathematics
This is a relative newcomer, established just ten years ago in 2013. CJM claims to:
publish papers of the highest quality, spanning the range of mathematics with an emphasis on pure mathematics.
Out of the 93 papers to date, it has published precisely Zero papers in Combinatorics. Yes, in Cambridge, MA which has the most active combinatorics seminar that I know (and used to co-organize twice a week). Perhaps, Combinatorics is not “pure” enough or simply lacks “papers of highest quality”.
Curiously, Jacob Fox is one of the seven “Associate Editors”. This makes me wonder about the CJM editorial policy, as in can any editor accept any paper they wish or the decision has to made by a majority of editors? Or, perhaps, each paper is accepted only by a unanimous vote? And how many Combinatorics papers were provisionally accepted only to be rejected by such a vote of the editorial board? Most likely, we will never know the answers…
The journal also had a mediocre record in Combinatorics until 2006 (12 papers out of 2661). None among the last 1172 papers (since 2007). Oh, my… I wrote in this blog post that at least the journal is honest about Combinatorics being low priority. But I think it still has no excuse. Read the following sentence on their front page:
Papers on other topics are welcome if they are of broad interest.
So, what happened in 2007? Papers in Combinatorics suddenly lost broad interest? Quanta Magazine must be really confused by this all…
(4) Publications Mathématiques de l’IHÉS
Very selective. Naturally. Zero papers in Combinatorics. Yes, since 1959 they published the grand total of 528 papers. No Combinatorics papers made the cut. I had a very limited interaction with the journal when I submitted my paper which was rejected immediately. Here is what I got:
Unfortunately, the journal has such a severe backlog that we decided at the last meeting of the editorial board not to take any new submissions for the next few months, except possibly for the solution of a major open problem. Because of this I prefer to reject you paper right now. I am sorry that your paper arrived during that period. [2015]
I am guessing the editor (very far from my area) assumed that the open problem that I resolved in that paper could not possibly be “major” enough. Because it’s in Combinatorics, you see… But whatever, let’s get back to ZERO. Really? In the past 50 years Paris has been a major research center in my area, one of the best places to do Enumerative, Asymptotics and Algebraic Combinatorics. And none of that work was deemed worthy by this venerable journal??
Note: I used this link for a quick guide to top journals. It’s biased, but really any other ranking would work just as well. I used the MathSciNet to determine whether papers are in Combinatorics (search for MSC Primary = 05)
How should we understand this?
It’s all about making an effort. Some leading general journals like Acta, Advances, Annals, Duke, Inventiones, JAMS, JEMS, Math. Ann., Math. Z., etc. found a way to attract and publish Combinatorics papers. Mind you they publish very few papers in the area, but whatever biases they have, they apparently want to make sure combinatorialists would consider sending their best work to these journals.
The four hall of shamers clearly found a way to repel papers in Combinatorics, whether by exhibiting an explicit bias, not having a combinatorialist on the editorial board, never encouraging best people in the area to submit, or using random people to give “quick opinions” on work far away from their area of expertise.
Most likely, there are several “grandfathered areas” in each journal, so with the enormous growth of submissions there is simply no room for other areas. Here is a breakdown of the top five areas in Publ. Math. IHES, helpfully compiled by ZbMATH (out of 528, remember?):

Of course, for the CJM, the whole “grandfathered areas” reasoning does not apply. Here is their breakdown of the top five areas (out of 93). See any similarities? Looks like this is a distribution of areas that the editors think are “very very important”:

When 2/3 of your papers are in just two areas, “spanning the range of mathematics” this journal is not. Of course, it really doesn’t matter how the four hall of shamers managed to achieve their perfect record for so many years — the results speak for themselves.
What should you do about it?
Not much, obviously, unless you are an editor in either of these four journals. Please don’t boycott them — it’s counterproductive and they are already boycotting you. If you work in Combinatorics, you should consider submitting your best work there, especially if you have tenure and have nothing to lose by waiting. This was the advice I gave vis-à-vie the Annals and it still applies.
But perhaps you can also shame these journals. This was also my advice on MDPI Mathematics. Here some strategy is useful, so perhaps do this. Any time you are asked for a referee report or for a quick opinion, ask the editor: Does your journal have a bias against Combinatorics? If they want your help they will say “No”. If you write a positive opinion or a report, follow up and ask if the paper is accepted. If they say “No”, ask if they still believe the journal has no bias. Aim to exhaust them!
More broadly, tell everyone you know that these four journals have an anti-Combinatorics bias. As I quoted before, Noga Alon thinks that “mathematics should be considered as one unit“. Well, as long as these journals don’t publish in Combinatorics, I will continue to disagree, and so should you. Finally, if you know someone on the editorial board of these four journals, please send them a link to this blog post and ask to write a comment. We can all use some explanation…
Innovation anxiety
I am on record of liking the status quo of math publishing. It’s very far from ideal as I repeatedly discuss on this blog, see e.g. my posts on the elitism, the invited issues, the non-free aspect of it in the electronic era, and especially the pay-to-publish corruption. But overall it’s ok. I give it a B+. It took us about two centuries to get where we are now. It may take us awhile to get to an A.
Given that there is room for improvement, it’s unsurprising that some people make an effort. The problem is that their efforts be moving us in the wrong direction. I am talking specifically about two ideas that frequently come up by people with best intensions: abolishing peer review and anonymizing the author’s name at the review stage. The former is radical, detrimental to our well being and unlikely to take hold in the near future. The second is already here and is simply misguided.
Before I take on both issues, let me take a bit of a rhetorical detour to make a rather obvious point. I will be quick, I promise!
Don’t steal!
Well, this is obvious, right? But why not? Let’s set all moral and legal issues aside and discuss it as adults. Why should a person X be upset if Y stole an object A from Z? Especially if X doesn’t know either Y or Z, and doesn’t really care who A should belong to. Ah, I see you really don’t want to engage with the issue — just like me you already know that this is appalling (and criminal, obviously).
However, if you look objectively at the society we live in, there is clearly some gray area. Indeed, some people think that taxation is a form of theft (“taking money by force”, you see). Millions of people think that illegally downloading movies is not stealing. My university administration thinks stealing my time making me fill all kinds of forms is totally kosher. The country where I grew up in was very proud about the many ways it stole my parents’ rights for liberty and the pursuit of happiness (so that they could keep their lives). The very same country thinks it’s ok to invade and steal territory from a neighboring country. Apparently many people in the world are ok with this (as in “not my problem”). Not comparing any of these, just challenging the “isn’t it obvious” premise.
Let me give a purely American answer to the “why not” question. Not the most interesting or innovative argument perhaps, but most relevant to the peer review discussion. Back in September 1789, Thomas Jefferson was worried about the constitutional precommitment. Why not, he wondered, have a revolution every 19 years, as a way not to burden future generations with rigid ideas from the past?
In February 1790, James Madison painted a grim picture of what would happen: “most of the rights of property would become absolutely defunct and the most violent struggles be generated” between property haves and have-nots, making remedy worse than the disease. In particular, allowing theft would be detrimental to continuing peaceful existence of the community (duh!).
In summary: a fairly minor change in the core part of the moral code can lead to drastic consequences.
Everyone hates peer review!
Indeed, I don’t know anyone who succeeded in academia without a great deal of frustration over the referee reports, many baseless rejections from the journals, or without having to spend many hours (days, weeks) writing their own referee reports. It’s all part of the job. Not the best part. The part well hidden from outside observers who think that professors mostly teach or emulate a drug cartel otherwise.
Well, the help is on the way! Every now and then somebody notably comes along and proposes to abolish the whole thing. Here is one, two, three just in the last few years. Enough? I guess not. Here is the most recent one, by Adam Mastroianni, twitted by Marc Andreessen to his 1.1 million followers.
This is all laughable, right? Well, hold on. Over the past two weeks I spoke to several well known people who think that abolishing peer review would make the community more equitable and would likely foster the innovation. So let’s address these objections seriously, point by point, straight from Mastroianni’s article.
(1) “If scientists cared a lot about peer review, when their papers got reviewed and rejected, they would listen to the feedback, do more experiments, rewrite the paper, etc. Instead, they usually just submit the same paper to another journal.” Huh? The same level journal? I wish…
(2) “Nobody cares to find out what the reviewers said or how the authors edited their paper in response” Oh yes, they do! Thus multiple rounds of review, sometimes over several years. Thus a lot of frustration. Thus occasional rejections after many rounds if the issue turns out non-fixable. That’s the point.
(3) “Scientists take unreviewed work seriously without thinking twice.” Sure, why not? Especially if they can understand the details. Occasionally they give well known people benefit of the doubt, at least for awhile. But then they email you and ask “Is this paper ok? Why isn’t it published yet? Are there any problems with the proof?” Or sometimes some real scrutiny happens outside of the peer review.
(4) “A little bit of vetting is better than none at all, right? I say: no way.” Huh? In math this is plainly ridiculous, but the author is moving in another direction. He supports this outrageous claim by saying that in biomedical sciences the peer review “fools people into thinking they’re safe when they’re not. That’s what our current system of peer review does, and it’s dangerous.” Uhm. So apparently Adam Mastroianni thinks if you can’t get 100% certainty, it’s better to have none. I feel like I’ve heard the same sentiment form my anti-masking relatives.
Obviously, I wouldn’t know and honestly couldn’t care less about how biomedical academics do research. Simply put, I trust experts in other fields and don’t think I know better than them what they do, should do or shouldn’t do. Mastroianni uses “nobody” 11 times in his blog post — must be great to have such a vast knowledge of everyone’s behavior. In any event, I do know that modern medical advances are nothing short of spectacular overall. Sounds like their system works really well, so maybe let them be…
The author concludes by arguing that it’s so much better to just post papers on the arXiv. He did that with one paper, put some jokes in it and people wrote him nice emails. We are all so happy for you, Adam! But wait, who says you can’t do this with all your papers in parallel with journal submissions? That’s what everyone in math does, at least the arXiv part. And if the journals where you publish don’t allow you to do that, that’s a problem with these specific journals, not with the whole peer review.
As for the jokes — I guess I am a mini-expert. Many of my papers have at least one joke. Some are obscure. Some are not funny. Some are both. After all, “what’s life without whimsy“? The journals tend to be ok with them, although some make me work for it. For example, in this recent paper, the referee asked me to specifically explain in the acknowledgements why am I thankful to Jane Austen. So I did as requested — it was an inspiration behind the first sentence (it’s on my long list of starters in my previous blog post). Anyway, you can do this, Adam! I believe in you!
Everyone needs peer review!
Let’s try to imagine now what would happen if the peer review is abolished. I know, this is obvious. But let’s game it out, post-apocaliptic style.
(1) All papers will be posted on the arXiv. In a few curious cases an informal discussion will emerge, like this one about this recent proof of the four color theorem. Most paper will be ignored just like they are ignored now.
(2) Without a neutral vetting process the journals will turn to publishing “who you know”, meaning the best known and best connected people in the area as “safe bets” whose work was repeatedly peer reviewed in the past. Junior mathematicians will have no other way to get published in leading journals without collaboration (i.e. writing “joint papers”) with top people in the area.
(3) Knowing that their papers won’t be refereed, people will start making shortcuts in their arguments. Soon enough some fraction will turn up unsalvageable incorrect. Embarrassments like the ones discussed in this page will become a common occurrence. Eventually the Atiyah-style proofs of famous theorems will become widespread confusing anyone and everyone.
(4) Granting agencies will start giving grants only to the best known people in the area who have most papers in best known journals (if you can peer review papers, you can’t expect to peer review grant proposals, right?) Eventually they will just stop, opting to give more money to best universities and institutions, in effect outsourcing their work.
(5) Universities will eventually abolish tenure as we know it, because if anyone is free to work on whatever they want without real rewards or accountability, what’s the point of tenure protection? When there are no objective standards, in the university hiring the letters will play the ultimate role along with many biases and random preferences by the hiring committees.
(6) People who work in deeper areas will be spending an extraordinary amount of time reading and verifying earlier papers in the area. Faced with these difficulties graduate students will stay away from such areas opting for more shallow areas. Eventually these areas will diminish to the point of near-extinsion. If you think this is unlikely, look into post-1980 history of finite group theory.
(7) In shallow areas, junior mathematicians will become increasingly more innovative to avoid reading older literature, but rather try to come up with a completely new question or a new theory which can be at least partially resolved on 10 pages. They will start running unrefereed competitive conferences where they will exhibit their little papers as works of modern art. The whole of math will become subjective and susceptible to fashion trends, not unlike some parts of theoretical computer science (TCS).
(8) Eventually people in other fields will start saying that math is trivial and useless, that everything they do can be done by an advanced high schooler in 15 min. We’ve seen this all before, think candid comments by Richard Feynman, or these uneducated proclamations by this blog’s old villain Amy Wax. In regards to combinatorics, such views were prevalent until relatively recently, see my “What is combinatorics” with some truly disparaging quotations, and this interview by László Lovász. Soon after, everyone (physics, economics, engineering, etc.) will start developing their own kind of math, which will be the end of the whole field as we know it.
…
(100) In the distant future, after the human civilization dies and rises up again, historians will look at the ruins of this civilization and wonder what happened? They will never learn that’s it’s all started with Adam Mastroianni when he proclaimed that “science must be free“.
Less catastrophic scenarios
If abolishing peer review does seem a little farfetched, consider the following less drastic measures to change or “improve” peer review.
(i) Say, you allow simultaneous submissions to multiple journals, whichever accepts first gets the paper. Currently, the waiting time is terribly long, so one can argue this would be an improvement. In support of this idea, one can argue that in journalism pitching a story to multiple editors is routine, that job applications are concurrent to all universities, etc. In fact, there is even an algorithm to resolve these kind of situations successfully. Let’s game this out this fantasy.
The first thing that would happen is that journals would be overwhelmed with submissions. The referees are already hard to find. After the change, they would start refusing all requests since they would also be overwhelmed with them and it’s unclear if the report would even be useful. The editors would refuse all but a few selected papers from leading mathematicians. Chat rooms would emerge in the style “who is refereeing which paper” (cf. PubPeer) to either collaborate or at least not make redundant effort. But since it’s hard to trust anonymous claims “I checked and there are no issues with Lemma 2 in that paper” (could that be the author?), these chats will either show real names thus leading to other complications (see below), or cease to exist.
Eventually the publishers will start asking for a signed official copyright transfer “conditional on acceptance” (some already do that), and those in violation will be hit with lawsuits. Universities will change their faculty code of conduct to include such copyright violations as a cause for dismissal, including tenure removal. That’s when the practice will stop and be back to normal, at great cost obviously.
(ii) Non-anonymizing referees is another perennial idea. Wouldn’t it be great if the referees get some credit for all the work that they do (so they can list it on their CVs). Even better if their referee report is available to the general public to read and scrutinize, etc. Win-win-win, right?
No, of course not. Many specialized sub-areas are small so it is hard to find a referee. For the authors, it’s relatively easy to guess who the referees are, at least if you have some experience. But there is still this crucial ambiguity as in “you have a guess but you don’t know for sure” which helps maintain friendship or at least collegiality with those who have written a negative referee report. You take away this ambiguity, and everyone will start refusing refereeing requests. Refereeing is hard already, there is really no need to risk collegial relationships as a result, especially in you are both going to be working the area for years or even decades to come.
(iii) Let’s pay the referees! This is similar but different from (ii). Think about it — the referees are hard to find, so we need to reward them. Everyone know that when you pay for something, everyone takes this more seriously, right? Ugh. I guess I have some new for you…
Think it over. You got a technical 30 page paper to referee. How much would you want to get paid? You start doing a mental calculation. Say, at a very modest $100/hr it would take you maybe 10-20 hours to write a thorough referee report. That’s $1-2K. Some people suggest $50/hr but that was before the current inflation. While I do my own share of refereeing, personally, I would charge more per hour as I can get paid better doing something else (say, teach our Summer school). For a traditional journal to pay this kind of money per paper is simply insane. Their budgets are are relatively small, let me spare you the details.
Now, who can afford that kind of money? Right — we are back to the open access journals who would pass the cost to the authors in the form of an APC. That’s when the story turn from bad to awful. For that kind of money the journals would want a positive referee report since rejected authors don’t pay. If you are not willing to play ball and give them a positive report, they will stop inviting you to referee, leading to more even corruption these journals have in the form of pay-to-publish.
You can probably imagine that this won’t end well. Just talk to medical or biological scientists who grudgingly pays to Nature or Science about 3K from their grants (which are much larger than ours). The pay because they have to, of course, and if they bulk they might not get a new grant setting back their career.
Double blind refereeing
In math, this means that the authors’ names are hidden from referees to avoid biases. The names are visible to the editors, obviously, to prevent “please referee your own paper” requests. The authors are allowed to post their papers on their websites or the arXiv, where it could be easily found by the title, so they don’t suffer from anxieties about their career or competitive pressures.
Now, in contrast with other “let’s improve the peer review” ideas, this is already happening. In other fields this has been happening for years. Closer to home, conferences in TCS have long resisted going double blind, but recently FOCS 2022, SODA 2023 and STOC 2023 all made the switch. Apparently they found Boaz Barak’s arguments unpersuasive. Well, good to know.
Even closer to home, a leading journal in my own area, Combinatorial Theory, turned double blind. This is not a happy turn of event, at least not from my perspective. I published 11 papers in JCTA, before the editorial board broke off and started CT. I have one paper accepted at CT which had to undergo the new double blind process. In total, this is 3 times as many as any other journal where I published. This was by far my favorite math journal.
Let’s hear from the journal why they did it (original emphasis):
The philosophy behind doubly anonymous refereeing is to reduce the effect of initial impressions and biases that may come from knowing the identity of authors. Our goal is to work together as a combinatorics community to select the most impactful, interesting, and well written mathematical papers within the scope of Combinatorial Theory.
Oh, sure. Terrific goal. I did not know my area has a bias problem (especially compared to many other areas), but of course how would I know?
Now, surely the journal didn’t think this change would be free? The editors must have compared pluses and minuses, and decided that on balance the benefits outweigh the cost, right? The journal is mum on that. If any serious discussion was conducted (as I was told), there is no public record of it. Here is what the journal says how the change is implemented:
As a referee, you are not disqualified to evaluate a paper if you think you know an author’s identity (unless you have a conflict of interest, such as being the author’s advisor or student). The journal asks you not to do additional research to identify the authors.
Right. So let me try to understand this. The referee is asked to make a decision whether to spend upwards of 10-20 hours on the basis of the first impression of the paper and without knowledge of the authors’ identity. They are asked not to google the authors’ names, but are ok if you do because they can’t enforce this ethical guideline anyway. So let’s think this over.
Double take on double blind
(1) The idea is so old in other sciences, there is plenty of research on its relative benefits. See e.g. here, there or there. From my cursory reading, it seems, there is a clear evidence of a persistent bias based on the reputation of educational institution. Other biases as well, to a lesser degree. This is beyond unfortunate. Collectively, we have to do better.
(2) Peer reviews have very different forms in different sciences. What works in some would not necessarily would work in others. For example, TCS conferences never really had a proper refereeing process. The referees are given 3 weeks to write an opinion of the paper based on the first 10 pages. They can read the proofs beyond the 10 pages, but don’t have to. They write “honest” opinions to the program committee (invisible to the authors) and whatever they think is “helpful” to the authors. Those of you outside of TCS can’t even imagine the quality and biases of these fully anonymous opinions. In recent years, the top conferences introduced the rebuttal stage which is probably helpful to avoid random superficial nitpicking at lengthy technical arguments.
In this large scale superficial setting with rapid turnover, the double blind refereeing is probably doing more good than bad by helping avoid biases. The authors who want to remain anonymous can simply not make their papers available for about three months between the submission and the decision dates. The conference submission date is a solid date stamp for them to stake the result, and three months are unlikely to make major change to their career prospects. OTOH, the authors who want to stake their reputation on the validity of their technical arguments (which are unlikely to be fully read by the referees) can put their papers on the arXiv. All in all, this seems reasonable and workable.
(3) The journal process is quite a bit longer than the conference, naturally. For example, our forthcoming CT paper was submitted on July 2, 2021 and accepted on November 3, 2022. That’s 16 months, exactly 490 days, or about 20 days per page, including the references. This is all completely normal and is nobody’s fault (definitely not the handling editor’s). In the meantime my junior coauthor applied for a job, was interviewed, got an offer, accepted and started a TT job. For this alone, it never crossed our mind not to put the paper on the arXiv right away.
Now, I have no doubt that the referee googled our paper simply because in our arguments we frequently refer our previous papers on the subject for which this was a sequel (er… actually we refer to some [CPP21a] and [CPP21b] papers). In such cases, if the referee knows that the paper under review is written by the same authors there is clearly more confidence that we are aware of the intricate parts of our own technical details from the previous paper. That’s a good thing.
Another good thing to have is the knowledge that our paper is surviving public scrutiny. Whenever issues arise we fix them, whenever some conjecture are proved or refuted, we update the paper. That’s a normal academic behavior no matter what Adam Mastroianni says. Our reputation and integrity is all we have, and one should make every effort to maintain it. But then the referee who has been procrastinating for a year can (and probably should) compare with the updated version. It’s the right thing to do.
Who wants to hide their name?
Now that I offered you some reasons why looking for paper authors is a good thing (at least in some cases), let’s look for negatives. Under what circumstances might the authors prefer to stay anonymous and not make their paper public on the arXiv?
(a) Junior researchers who are afraid their low status can reduce their chances to get accepted. Right, like graduate students. This will hurt them both mathematically and job wise. This is probably my biggest worry that CT is encouraging more such cases.
(b) Serial submitters and self-plagiarists. Some people write many hundreds of papers. They will definitely benefit from anonymity. The editors know who they are and that their “average paper” has few if any citations outside of self-citations. But they are in a bind — they have to be neutral arbiters and judge each new paper independently of the past. Who knows, maybe this new submission is really good? The referees have no such obligation. On the contrary, they are explicitly asked to make a judgement. But if they have no name to judge the paper by, what are they supposed to do?
Now, this whole anonymity thing is unlikely to help serial submitters at CT, assuming that the journal standards remain high. Their papers will be rejected and they will move on, submitting down the line until they find an obscure enough journal that will bite. If other, somewhat less selective journals adopt the double blind review practice, this could improve their chances, however.
For CT, the difference is that in the anonymous case the referees (and the editors) will spend quite a bit more time per paper. For example, when I know that the author is a junior researcher from a university with limited access to modern literature and senior experts, I go out of my way to write a detailed referee report to help the authors, suggest some literature they are missing or potential directions for their study. If this is a serial submitter, I don’t. What’s the point? I’ve tried this a few times, and got the very same paper from another journal next week. They wouldn’t even fix the typos that I pointed out, as if saying “who has the time for that?” This is where Mastroianni is right: why would their 234-th paper be any different from 233-rd?
(c) Cranks, fraudsters and scammers. The anonymity is their defense mechanism. Say, you google the author and it’s Dănuț Marcu, a serial plagiarist of 400+ math papers. Then you look for a paper he is plagiarizing from and if successful making efforts to ban him from your journal. But if the author is anonymous, you try to referee. There is a very good chance you will accept since he used to plagiarize good but old and somewhat obscure papers. So you see — the author’s identity matters!
Same with the occasional zero-knowledge (ZK) aspirational provers whom I profiled at the end of this blog post. If you are an expert in the area and know of somebody who has tried for years to solve a major conjecture producing one false or incomplete solution after another, what do you do when you see a new attempt? Now compare with what you do if this paper is by anonymous? Are you going to spend the same effort effort working out details of both papers? Wouldn’t in the case of a ZK prover you stop when you find a mistake in the proof of Lemma 2, while in the case of a genuine new effort try to work it out?
In summary: as I explained in my post above, it’s the right thing to do to judge people by their past work and their academic integrity. When authors are anonymous and cannot be found, the losers are the most vulnerable, while the winners are the nefarious characters. Those who do post their work on the arXiv come out about even.
Small changes can make a major difference
If you are still reading, you probably think I am completely 100% opposed to changes in peer review. That’s not true. I am only opposed to large changes. The stakes are just too high. We’ve been doing peer review for a long time. Over the decades we found a workable model. As I tried to explain above, even modest changes can be detrimental.
On the other hand, very small changes can be helpful if implemented gradually and slowly. This is what TCS did with their double blind review and their rebuttal process. They started experimenting with lesser known and low stakes conferences, and improved the process over the years. Eventually they worked out the kinks like COI and implemented the changes at top conferences. If you had to make changes, why would you start with a top journal in the area??
Let me give one more example of a well meaning but ultimately misguided effort to make a change. My former Lt. Governor Gavin Newsom once decided that MOOCs are the answer to education foes and is a way for CA to start giving $10K Bachelor’s degrees. The thinking was — let’s make a major change (a disruption!) to the old technology (teaching) in the style of Google, Uber and Theranos!
Lo and behold, California spent millions and went nowhere. Our collective teaching experience during COVID shows that this was not an accident or mismanagement. My current Governor, the very same Gavin Newsom, dropped this idea like a rock, limiting it to cosmetic changes. Note that this isn’t to say that online education is hopeless. In fact, see this old blog post where I offer some suggestions.
My modest proposal
The following suggestions are limited to pure math. Other fields and sciences are much too foreign for me to judge.
(i) Introduce a very clearly defined quick opinion window of about 3-4 weeks. The referees asked for quick opinions can either decline or agree within 48 hours. It will only take them about 10-20 minutes to make an opinion based on the introduction, so give them a week to respond with 1-2 paragraphs. Collect 2-3 quick opinions. If as an editor you feel you need more, you are probably biased against the paper or the area, and are fishing for a negative opinion to have “quick reject“. This is a bit similar to the way Nature, Science, etc. deal with their submissions.
(ii) Make quick opinion requests anonymous. Request the reviewers to assess how the paper fits the journal (better, worse, on point, best submitted to another area to journals X, Y or Z, etc.) Adopt the practice of returning these opinions to the authors. Proceed to the second stage by mutual agreement. This is a bit similar to TCS which has authors use the feedback from the conference makes decisions about the journal or other conference submissions.
(iii) If the paper is rejected or withdrawn after the quick opinion stage, adopt the practice to send quick opinions to another journal where the paper is resubmitted. Don’t communicate the names of the reviewers — if the new editor has no trust in the first editor’s qualifications, let them collect their own quick opinions. This would protect the reviewers from their names going to multiple journals thus making their names semi-public.
(iv) The most selective journals should require that the paper not be available on the web during the quick opinion stage, and violators be rejected without review. Anonymous for one — anonymous for all! The three week long delay is unlikely to hurt anybody, and the journal submission email confirmation should serve as a solid certificate of a priority if necessary. Some people will try to game the system like give a talk with the same title as the paper or write a blog post. Then it’s on editor’s discretion what to do.
(v) In the second (actual review) stage, the referees should get papers with authors’ names and proceed per usual practice.
Happy New Year everyone!
What to publish?
This might seem like a strange question. A snarky answer would be “everything!” But no, not really everything. Not all math deserves to be published, just like not all math needs to be done. Making this judgement is difficult and goes against the all too welcoming nature of the field. But if you want to succeed in math as a profession, you need to make some choices. This is a blog post about the choices we make and the choices we ought to make.
Bedtime questions
Suppose you tried to solve a major open problem. You failed. A lot of time is wasted. Maybe it’s false, after all, who knows. You are no longer confident. But you did manage to compute some nice examples, which can be turned into a mediocre little paper. Should you write it and post it on the arXiv? Should you submit it to a third rate journal? A mediocre paper is still a consolation prize, right? Better than nothing, no?
Or, perhaps, it is better not to show how little you proved? Wouldn’t people judge you as an “average” of all published papers on your CV? Wouldn’t this paper have negative impact on your job search next year? Maybe it’s better to just keep it to yourself for now and hope you can make a breakthrough next year? Or some day?
But wait, other people in the area have a lot more papers. Some are also going to be on a job market next year. Shouldn’t you try to catch up and publish every little thing you have? People at other universities do look at the numbers, right? Maybe nobody will notice this little paper. If you have more stuff done by then it will get lost in the middle of my CV, but it will help get the numbers up. Aren’t you clever or what?
Oh, wait, maybe not! You do have to send your CV to your letter writers. They will look at all your papers. How would they react to a mediocre paper? Will they judge you badly? What in the world should you do?!?
Well, obviously I don’t have one simple answer to that. But I do have some thoughts. And this quote from a famous 200 year old Russian play about people who really cared how they are perceived:
Chatsky: I wonder who the judges are! […]
Famusov: My goodness! What will countess Marya Aleksevna say to this?
[Alexander Griboyedov, Woe from Wit, 1823, abridged.]
You would think our society had advanced at least a little…
Who are the champions?
If we want to find the answers to our questions, it’s worth looking at the leaders of the field. Let’s take a few steps back and simply ask — Who are the best mathematicians? Ridiculous questions always get many ridiculous answers, so here is a random ranking by some internet person: Newton, Archimedes, Gauss, Euler, etc. Well, ok — these are all pretty dead and probably never had to deal with a bad referee report (I am assuming).
Here is another random list, from a well named website research.com. Lots of living people finally: Barry Simon, Noga Alon, Gilbert Laporte, S.T. Yau, etc. Sure, why not? But consider this recent entrant: Ravi P. Agarwal is at number 20, comfortably ahead of Paul Erdős at number 25. Uhm, why?

Or consider Theodore E. Simos who is apparently the “Best Russian Mathematician” according to research.com, and number 31 in the world ranking:
Uhm, I know MANY Russian mathematicians. Some of them are truly excellent. Who is this famous Simos I never heard of? How come he is so far ahead of Vladimir Arnold who is at number 829 on the list?

Of course, you already guessed the answer. It’s obvious from the pictures above. In their infinite wisdom, research.com judges mathematicians by the weighted average of the numbers of papers and citations. Arnold is doing well on citations, but published so little! Only 157 papers!
Numbers rule the world
To dig a little deeper into this citation phenomenon, take a look at the following curious table from a recent article “Extremal mathematicians“ by Carlos Alfaro:
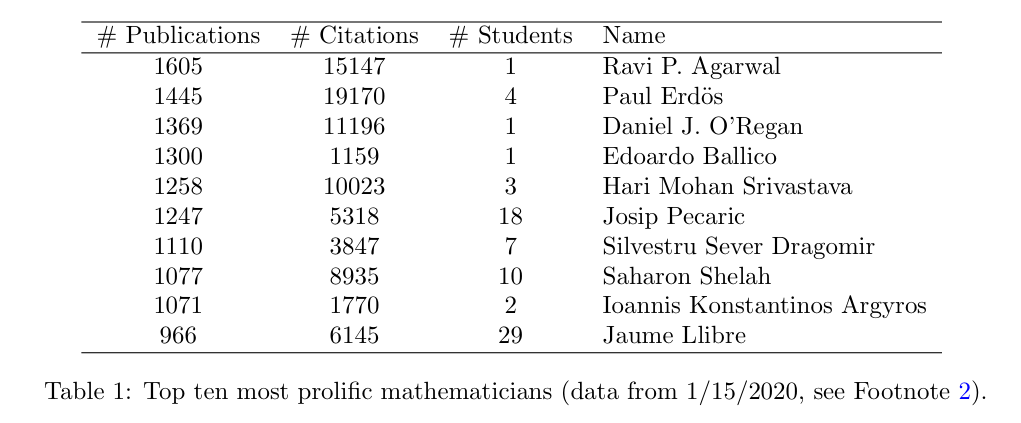
If you’ve been in the field for awhile, you are probably staring at this in disbelief. How do you physically write so many papers?? Is this even true???
Yes, you know how Paul Erdős did it — he was amazing and he had a lot of coauthors. No, you don’t know how Saharon Shelah does it. But he is a legend, and you are ok with that. But here we meet again our hero Ravi P. Agarwal, the only human mathematician with more papers than Erdős. Who is he? Here is what the MathSciNet says:

Note that Ravi is still going strong — in less than 3 years he added 125 papers. Of these 1727 papers, 645 are with his favorite coauthor Donal O’Regan, number 3 on the list above. Huh? What is going on??
What’s in a number?
If the number of papers is what’s causing you to worry, let’s talk about it. Yes, there is also number of citations, the h-index (which boils down to the number of citations anyway), and maybe other awful measurements of research productivity. But the number of papers is what you have a total control over. So here are a few strategies how you can inflate the number that I learned from a close examination of publishing practices of some of the “extremal mathematicians”. They are best employed in combination:
(a) Form a clique. Over the years build a group of 5-8 close collaborators. Keep writing papers in different subsets of 3-5 of them. This is easier to do since each gets to have many papers while writing only a fraction. Make sure each papers cites heavily all other subsets from the clique. To an untrained eye of an editor, these would appear to be experts who are able to referee the paper.
(b) Form a cartel. This is a strong for of a clique. Invent an area and call yourselves collaborative research in that area. Make up a technical name, something like “analytic and algebraic topology
of locally Euclidean metrizations of infinitely differentiable Riemannian manifolds“. Apply for collaborative grants, organize conferences, publish conference proceedings, publish monographs, start your own journal. From outside it looks like a normal research activity, and who is to judge after all?
(c) Publish in little known, not very selective or shady journals. For example, Ravi P. Agarwal published 26 papers in Mathematics (MDPI Journal) that I discussed at length in this blog post. Note aside: since Mathematics is not indexed by the MathSciNet, the numbers above undercount his total productivity.
(d) Organize special issues with these journals. For example, here is a list of 11(!) special issues Agarwal served as a special editor with MDPI. Note the breadth of the collection:

(e) Become an editor of an established but not well managed journal and publish a lot there with all your collaborators. For example, T.E. Simos has a remarkable record of 150 (!) papers in the Journal of Mathematical Chemistry, where he is an editor. I feel that Springer should be ashamed of such a poor oversight of this journal, but nothing can be done I am sure since the journal has a healthy 2.413 impact factor, and Simos’s hard work surely contributed to its rise from just 1.056 in 2015. OTOH, maybe somebody can convince the MathSciNet to stop indexing this journal?

Let me emphasize that nothing on the list above is unethical, at least in a way the AMS or the NAS define these (as do most universities I think). The difference is quantitative, not qualitative. So these should not be conflated with various paper mill practices such as those described in this article by Anna Abalkina.
Disclaimer: I strongly recommend you use none of these strategies. They are abusing the system and have detrimental long term effects to both your area and your reputation.
Zero-knowledge publishing
In mathematics, there is another method of publishing that I want to describe. This one is borderline unethical at best, so I will refrain from naming names. You figure it out on your own!
Imagine you want to prove a major open problem in the area. More precisely, you want to become famous for doing that without actually getting the proof. In math, you can’t get there without publishing your “proof” in a leading area journal, better yet one of the top journals in mathematics. And if you do, it’s a good bet the referees will examine your proof very carefully. Sounds like a fail-proof system, right?
Think again! Here is an ingenuous strategy that I recently happen to learn. The strategy is modeled on the celebrated zero-knowledge proof technique, although the author I am thinking of might not be aware of that.
For simplicity, let’s say the open problem is “A=? Z”. Here is what you do, step by step.
- You come up with a large set of problems P,Q,R,S,T,U,V,W,X,Y which are all equivalent to Z. You then start a well publicized paper factory proving P=Q, W=X, X=Z, Q=Z, etc. All these papers are correct and give a good vibe of somebody who is working hard on the A=?Z problem. Make sure you have a lot of famous coauthors on these papers to further establish your credibility. In haste, make the papers barely readable so that the referees don’t find any major mistakes but get exhausted by the end.
- Make another list of problems B,C,D,E,F,G which are equivalent to A. Keep these equivalences secret. Start writing new papers proving B=T, D=Y, E=X, etc. Write them all in a style similar to previous list: cumbersome, some missing details, errors in minor arguments, etc. No famous people as coauthors. Do try to involve many grad students and coauthors to generate good will (such a great mentor!) They will all be incorrect, but none of them would raise a flag since by themselves they don’t actually prove A=Z.
- Populate the arXiv with all these papers and submit them to different reputable journals in the area. Some referees or random readers will find mistakes, so you fix one incomprehensible detail with another and resubmit. If crucial problems in one paper persist, just drop it and keep going through the motions on all other papers. Take your time.
- Eventually one of these will get accepted because the referees are human and they get tired. They will just assume that the paper they are handling is just like the papers on the first list – clumsily written but ultimately correct. And who wants to drag things down over some random reduction — the young researcher’s career is on the line. Or perhaps, the referee is a coauthor of some of the paper on the first list – in this case they are already conditioned to believe the claims because that’s what they learned from the experience on the joint paper.
- As soon as any paper from the second list is accepted, say E=X, take off the shelf the reduction you already know and make it public with great fanfare. For example, in this case quickly announce that A=E. Combined with the E=X breakthrough, and together with X=W and W=Z previously published in the first list, you can conclude that A=Z. Send it to the Annals. What are the referees going to do? Your newest A=E is inarguable, clearly true. How clever are you to have figured out the last piece so quickly! The other papers are all complicated and confusing, they all raise questions, but somebody must have refereed them and accepted/published them. Congratulations on the solution of A=Z problem! Well done!
It might take years or even decades until the area has a consensus that one should simply ignore the erroneous E=X paper and return to “A=?Z” the status of an open problem. The Annals will refuse to publish a retraction — technically they only published a correct A=E reduction, so it’s all other journals’ fault. It will all be good again, back to normal. But soon after, new papers such as G=U and B=R start to appear, and the agony continues anew…
From math to art
Now that I (hopefully) convinced you that high numbers of publications is an achievable but ultimately futile goal, how should you judge the papers? Do they at least make a nonnegative contribution to one’s CV? The answer to the latter question is “No”. This contribution can be negative. One way to think about is by invoking the high end art market.
Any art historian would be happy to vouch that the worth of a painting hinges heavily on the identity of the artist. But why should it? If the whole purpose of a piece of art is to evoke some feelings, how does the artist figures into this formula? This is super naïve, obviously, and I am sure you all understand why. My point is that things are not so simple.
One way to see the a pattern among famous artists is to realize that they don’t just create “one off” paintings, but rather a “series”. For example, Monet famously had haystack and Rouen Cathedral series, Van Gogh had a sunflowers series, Mondrian had a distinctive style with his “tableau” and “composition” series, etc. Having a recognizable very distinctive style is important, suggesting that painting in series are valued differently than those that are not, even if they are by the same artist.
Finally, the scarcity is an issue. For example Rodin’s Thinker is one of the most recognizable sculptures in the world. So is the Celebration series by Jeff Koons. While the latter keep fetching enormous prices at auctions, the latest sale of a Thinker couldn’t get a fifth of the Yellow Balloon Dog price. It could be because balloon animals are so cool, but could also be that there are 27 Thinkers in total, all made from the same cast. OTOH, there are only 5 balloon dogs, and they all have distinctly different colors making them both instantly recognizable yet still unique. You get it now — it’s complicated…
What papers to write
There isn’t anything objective of course, but thinking of art helps. Let’s figure this out by working backward. At the end, you need to be able to give a good colloquium style talk about your work. What kid of papers should you write to give such a talk?
- You can solve a major open problem. The talk writes itself then. You discuss the background, many famous people’s attempts and partial solutions. Then state your result and give an idea of the proof. Done. No need to have a follow up or related work. Your theorem speaks for itself. This is analogous to the most famous paintings. There are no haystacks or sunflowers on that list.
- You can tell a good story. I already wrote about how to write a good story in a math paper, and this is related. You start your talk by telling what’s the state of the sub-area, what are the major open problems and how do different aspects of your work fit in the picture. Then talk about how the technology that you develop over several papers positioned you to make a major advance in the area that is your most recent work. This is analogous to the series of painting.
- You can prove something small and nice, but be an amazing lecturer. You mesmerize the audience with your eloquence. For about 5 minutes after your talk they will keep thinking this little problem you solved is the most important result in all of mathematics. This feeling will fade, but good vibes will remain. They might still hire you — such talent is rare and teaching excellence is very valuable.
That’s it. If you want to give a good job talk, there is no other way to do it. This is why writing many one-off little papers makes very little sense. A good talk is not a patchwork quilt – you can’t make it of disparate pieces. In fact, I heard some talks where people tried to do that. They always have coherence of a portrait gallery of different subjects by different artists.
Back to the bedtime questions — the answer should be easy to guess now. If your little paper fits the narrative, do write it and publish it. If it helps you tell a good story — that sounds great. People in the area will want to know that you are brave enough to make a push towards a difficult problem using the tools or results you previously developed. But if it’s a one-off thing, like you thought for some reason that you could solve a major open problem in another area — why tell anyone? If anything, this distracts from the story you want to tell about your main line of research.
How to judge other people’s papers
First, you do what you usually do. Read the paper, make a judgement on the validity and relative importance of the result. But then you supplement the judgement with what you know about the author, just like when you judge a painting.
This may seem controversial, but it’s not. We live in an era of thousands of math journals which publish in total over 130K papers a year (according to MathSciNet). The sheer amount of mathematical research is overwhelming and the expertise has fractured into tiny sub-sub-areas, many hundreds of them. Deciding if a paper is a useful contribution to the area is by definition a function of what the community thinks about the paper.
Clearly, you can’t poll all members of the community, but you can ask a couple of people (usually called referees). And you can look at how previous papers by the author had been accepted by the community. This is why in the art world they always write about recent sales: what money and what museum or private collections bought the previous paintings, etc. Let me give you some math examples.
Say, you are an editor. Somebody submits a bijective proof of a binomial identity. The paper is short but nice. Clearly publishable. But then you check previous publications and discover the author has several/many other published papers with nice bijective proofs of other binomial identities, and all of them have mostly self-citations. Then you realize that in the ocean of binomial identities you can’t even check if this work has been done before. If somebody in the future wants to use this bijection, how would they go about looking for it? What will they be googling for? If you don’t have good answers to these questions, why would you accept such a paper then?
Say, you are hiring a postdoc. You see files of two candidates in your area. Both have excellent well written research proposals. One has 15 papers, another just 5 papers. The first is all over the place, can do and solve anything. The second is studious and works towards building a theory. You only have time to read the proposals (nobody has time to read all 20 papers). You looks at the best papers of each and they are of similar quality. Who do you hire?
That depends on who you are looking for, obviously. If you are a fancy shmancy university where there are many grad students and postdocs all competing with each other, none working closely with their postdoc supervisor — probably the first one. Lots of random papers is a plus — the candidate clearly adapts well and will work with many others without need for a supervision. There is even a chance that they prove something truly important, it’s hard to say, right? Whether they get a good TT job afterwards and what kind of job would that be is really irrelevant — other postdocs will be coming in a steady flow anyway.
But if you want to have this new postdoc to work closely with a faculty at your university, someone intent on building a something valuable, so that they are able to give a nice job talk telling a good story at the end, hire the second one. They first is much too independent and will probably be unable to concentrate on anything specific. The amount of supervision tends to go less, not more, as people move up. Left to their own devices you expect from these postdocs more of the same, so the choice becomes easy.
Say, you are looking at a paper submitted to you as an editor of an obscure journal. You need a referee. Look at the previous papers by the authors and see lots of the repeated names. Maybe it’s a clique? Make sure your referees are not from this clique, completely unrelated to them in any way.
Or, say, you are looking at a paper in your area which claims to have made an important step towards resolving a major conjecture. The first thing you do is look at previous papers by the same person. Have they said the same before? Was it the same or a different approach? Have any of their papers been retracted or major mistakes found? Do they have several parallel papers which prove not exactly related results towards the same goal? If the answer is Yes, this might be a zero-knowledge publishing attempt. Do nothing. But do tell everyone in the area to ignore this author until they publish one definitive paper proving all their claims. Or not, most likely…
P.S. I realize that many well meaning journals have double blind reviews. I understand where they are coming from, but think in the case of math this is misguided. This post is already much too long for me to talk about that — some other time, perhaps.
Are we united in anything?
Unity here, unity there, unity shmunity is everywhere. You just can’t avoid hearing about it. Every day, no matter the subject, somebody is going to call for it. Be it in Ukraine or Canada, Taiwan or Haiti, everyone is calling for unity. President Biden in his Inaugural Address called for it eight times by my count. So did former President Bush on every recent societal issue: here, there, everywhere. So did Obama and Reagan. I am sure just about every major US politician made the same call at some point. And why not? Like the “world peace“, the unity is assumed to be a universal good, or at least an inspirational if quickly forgettable goal.
Take the Beijing Olympic Games, which proudly claims that their motto “demonstrates unity and a collective effort” towards “the goal of pursuing world unity, peace and progress”. Come again? While The New York Times isn’t buying the whole “world unity” thing and calls the games “divisive” it still thinks that “Opening Ceremony [is] in Search of Unity.” Vox is also going there, claiming that the ceremony “emphasized peace, world unity, and the people around the world who have battled the pandemic.” So it sounds to me that despite all the politics, both Vox and the Times think that this mythical unity is something valuable, right? Well, ok, good to know…
Closer to home, you see the same themes said about the International Congress of Mathematicians to be held in St. Petersburg later this year. Here is Arkady Dvorkovich, co-chair of the Executive Organizing Committee and former Deputy Prime Minister of Russia: “It seems to us that Russia will be able to truly unite mathematicians from all over the world“. Huh? Are you sure? Unite in what exactly? Because even many Russian mathematicians are not on board with having the ICM in St. Petersburg. And among those from “all over the world”, quite a few are very openly boycotting the congress, so much that even the IMU started to worry. Doesn’t “unity” mean “for all”, as in ∀?
Unity of mathematics
Frequent readers of this blog can probably guess where I stand on the “unity”. Even in my own area of Combinatorics, I couldn’t find much of it at all. I openly mocked “the feeling of unity of mathematics” argument in favor of some conjectures. I tried but could never understand Noga Alon’s claim that “mathematics should be considered as one unit” other than a political statement by a former PC Chair of the 2006 ICM.
So, about this “unity of mathematics”. Like, really? All of mathematics? Quick, tell me what exactly do the Stochastic PDEs, Algebraic Number Theory, Enumerative Combinatorics and Biostatistics have in common? Anything comes to mind? Anything at all? Ugh. Let’s make another experiment. Say, I tell you that only two of these four areas have Fields medals. Can you guess which ones? Oh, you can? Really, it was that easy?? Doesn’t this cut against all of this alleged “unity”?
Anyway, let’s be serious. Mathematics is not a unit. It’s not even a “patterned tapestry” of connected threads. It’s a human endeavor. It’s an assorted collection of scientific pursuits unconstrained by physical experiments. Some of them are deep, some shallow, some are connected to others, and some are motivated by real world applications. You check the MSC 2020 classification, and there is everything under the sun, 224 pages in total. It’s preposterous to look for and expect to find some unity there. There is none to be found.
Let me put it differently. Take poetry. Like math, it’s a artistic endeavor. Poems are written by the people and for the people. To enjoy. To recall when in need or when in a mood. Like math papers. Now, can anyone keep a straight face and say “unity of poetry“? Of course not. If anything, it’s the opposite. In poetry, having a distinctive voice is celebrated. Diverse styles are lauded. New forms are created. Strong emotions are evoked. That’s the point. Why would math be any different then?
What exactly unites us?
Mathematicians, I mean. Not much, I suppose, to the contrary of math politicians’ claims:
I like to think that increasing breadth in research will help the mathematical sciences to recognize our essential unity. (Margaret Wright, SIAM President, 1996)
Huh? Isn’t this like saying that space exploration will help foster cross-cultural understanding? Sounds reasonable until you actually think about what is being said…
Even the style of doing research is completely different. Some prove theorems, some make heavy computer computations, some make physical experiments, etc. At the end, some write papers and put them on the arXiv, some write long books full of words (e.g. mathematical historians), some submit to competitive conferences (e.g. in theoretical computer science), some upload software packages and experimental evidence to some data depositary. It’s all different. Don’t be alarmed, this is normal.
In truth, very little unites us. Some mathematicians work at large state universities, others at small private liberal arts colleges with a completely different approach to teaching. Some have a great commitment to math education, some spend every waking hour doing research, while others enjoy frequent fishing trips thanks to tenure. Some go into university administration or math politics, while others become journal editors.
In truth, only two things unites us — giant math societies like the AMS and giant conferences like ICMs and joint AMS/MAA/SIAM meetings. Let’s treat them separately, but before we go there, let’s take a detour just to see what an honest unrestricted public discourse sounds like:
What to do about the Olympics
The answer depends on who you ask, obviously. And opinions are abound. I personally don’t care other than the unfortunate fact that 2028 Olympics will be hosted on my campus. But we in math should learn how to be critical, so here is a range of voices that I googled. Do with them as you please.
Some are sort of in favor:
I still believe the Olympics contribute a net benefit to humanity. (Beth Daley, The Conversation, Feb. 2018)
Some are positive if a little ambivalent:
The Games aren’t dead. Not by a longshot. But it’s worth noting that the reason they are alive has strikingly little to do with games, athletes or medals. (L. Jon Wertheim, Time, June 2021)
Some like The New York Times are highly critical, calling it “absurdity”. Some are blunt:
More and more, the international spectacle has become synonymous with overspending, corruption, and autocratic regimes. (Yasmeen Serhan, The Atlantic, Aug. 2021)
yet unwilling to make the leap and call it quits. Others are less shy:
You can’t reform the Olympics. The Olympics are showing us what they are, and what they’ve always been. (Gia Lappe and Jonny Coleman, Jacobin, July 2021)
and
Boil down all the sanctimonious drivel about how edifying the games are, and you’re left with the unavoidable truth: The Olympics wreck lives. (Natalie Shure, The New Republic, July 2021)
What is the ICM
Well, it’s a giant collective effort. A very old tradition. Medals are distributed. Lots of talks. Speakers are told that it’s an honor to be chosen. Universities issue press releases. Yes, like this one. Rich countries set up and give away travel grants. Poor countries scramble to pay for participants. The host country gets dubious PR benefits. A week after it’s over everyone forgets it ever happened. Life goes on.
I went to just one ICM, in Rio in 2018. It was an honor to be invited. But the experience was decidedly mixed. The speakers were terrific mathematicians, all of them. Many were good speakers. A few were dreadful in both content and style. Some figured they are giving talks in their research seminar rather than to a general audience, so I left a couple of such talks in middle. Many talks in parallel sections were not even recorded. What a shame!
The crowds were stupefying. I saw a lot of faces. Some were friendly, of people I hadn’t seen in years, sometimes 20 years. Some were people I knew only by name. It was nice to say hello, to shake their hand. But there were thousands more. Literally. An ocean of people. I was drowning. This was the worst place for an introvert.
While there, I asked a lot of people how did they like the ICM. Some were electrified by the experience and had a decent enough time. Some looked like fish out of the water — when asked they just stared at me incomprehensively silently saying “What are you, an idiot?” Some told me they just went to the opening ceremony and left for the beach for the rest of the ICM. Assaf Naor said that he loved everything. I was so amused by that, I asked if I could quote him. “Yes,” he said, “you can quote me: I loved absolutely every bit of the ICM”. Here we go — not everyone is an introvert.
Whatever happened at the ICM
Unlike the Olympics, math people tend to be shy in their ICM criticism. In his somewhat unfortunately titled but otherwise useful historical book “Mathematicians of the World, Unite!” the author, Guillermo Curbera, largely stays exuberant about the subject. He does mention some critical stories, like this one:
Charlotte Angas Scott reported bluntly on the presentation of papers in the congress, which in her opinion were “usually shockingly bad” since “instead of speaking to the audience, [the lecturer] reads his paper to himself in a monotone that is sometimes hurried, sometimes hesitating, and frequently bored . . . so that he is often tedious and incomprehensible.” (Paris 1900 Chapter, p. 24)
Curbera does mention in passing that the were some controversies: Grothendieck refused to attend ICM Moscow in 1966 for political reasons, Margulis and Novikov were not allowed by the Soviet Union to leave the country to receive their Fields medals. Well, nobody’s perfect, right?
Most reports I found on the web are highly positive. Read, for example, Gil Kalai’s blog posts on the ICM 2018. Everything was great, right? Even Doron Zeilberger, not known for holding his tongue, is mostly positive (about the ICM Beijing in 2002). He does suggest that the invited speakers “should go to a ‘training camp‘” for some sort of teacher training re-education, apparently not seeing the irony, or simply under impression of all those great things in Beijing.
The only (highly controversial) criticism that I found was from Ulf Persson who starts with:
The congresses are by now considered to be monstrous affairs very different from the original intimate gatherings where group pictures could be taken.
He then continues to talk about various personal inconveniences, his misimpressions about the ICM setting, the culture, the city, etc., all in a somewhat insensitive and rather disparaging manner. Apparently, this criticism and misimpressions earned a major smackdown from Marcelo Viana, the ICM 2018 Organizing Committee Chair, who wrote that this was a “piece of bigotry” by somebody who is “poorly informed”. Fair enough. I agree with that and with the EMS President Volker Mehrmann who wrote in the same EMS newsletter that the article was “very counterproductive”. Sure. But an oversized 4 page reaction to an opinion article in a math newsletter from another continent seem indicative that the big boss hates criticism. Because we need all that “unity”, right?
Anyway, don’t hold your breath to see anything critical about the ICM St. Petersburg later this year. Clearly, everything is going to be just fantastic, nothing controversial about it. Right…
What to do about the ICM
Stop having them in the current form. It’s the 21st century, and we are starting the third year of the pandemic. All talks can be moved online so that everyone can watch them either as they happen, or later on YouTube. Let me note that I’ve sat in the bleachers of these makeshift 1000+ people convention center auditoriums where the LaTeX formulas are barely visible. This is what the view is like:

Note that the ICM is not like a sports event — there is literally nothing at stake. Also, there are usually no questions afterwards anyway. You are all better off watching the talks later on your laptop, perhaps even on a x1.5 speed. To get the idea, imagine watching this talk in a huge room full of people…. Even better, we can also spread out these online lectures across the time zones so that people from different countries can participate. Something like this World Relay in Combinatorics.
Really, all that CO2 burned to get humans halfway across the world to seat in a crowded space is not doing anyone any good. If the Nobel Prizes can be awarded remotely, so can the Fields medals. Tourism value aside, the amount of meaningful person-to-person interaction is so minimal in a large crowd, I am struggling to find a single good reason at all to have these extravaganzas in-person.
What to do about the AMS
I am not a member of any math societies so it’s not my place to tell them what to do. As a frequent contributor to AMS journals and a former editor of one of them, I did call on the AMS to separate its society business form the publishing, but given that their business model hinges on the books and journals they sell, this is unlikely. Still, let me make some quick observations which might be helpful.
The AMS is clearly getting less and less popular. I couldn’t find the exact membership numbers, but their “dues and outreach” earnings have been flat for a while. Things are clearly not going in the right direction, so much that the current AMS President Ruth Charney sent out a survey earlier this week asking people like me why do we not want to join.
People seem to realize that they have many different views on all thing math related and are seeking associations which are a better fit. One notable example is the Just Mathematics Collective which has several notable boycott initiatives. Another is the Association for Mathematical Research formed following various controversies. Note that there is a great deal of disagreements between these two, see e.g. here, there and there.
I feel these are very good developments. It’s healthy to express disagreements on issues you consider important. And while I disagree with other things in the article below, I do agree with this basic premise:
Totalitarian countries have unity. Democratic republics have disagreement. (Kevin Williamson, Against Unity, National Review, Jan. 2021)
So everyone just chill. Enjoy diverse views and opinions. Disagree with the others. And think twice before you call for “unity” of anything, or praise the ephemeral “unity of mathematics”. There is none.
My interview
Readers of this blog will remember my strong advocacy for taking interviews. In a surprising turn of events, Toufik Mansour interviewed me for the journal Enumerative Combinatorics and Applications (ECA). Here is that interview. Not sure if I am the right person to be interviewed, but if you want to see other Toufik’s interviews — click here (I mentioned some of them earlier). I am looking forward to read interviews of many more people in ECA and other journals.
P.S. The interview asks also about this blog, so it seems fitting to mention it here.
Corrections: (March 11, 2021) 1. I misread “What three results do you consider the most influential in combinatorics during the last thirty years?” question as asking about my own three results that are specifically in combinatorics. Ugh, to the original question – none of my results would go on that list. 2. In the pattern avoidance question, I misstated the last condition: I am asking for ec(Π) to be non-algebraic. Sorry everyone for all the confusion!
How to tell a good mathematical story
As I mentioned in my previous blog post, I was asked to contribute to to the Early Career Collection in the Notices of the AMS. The paper is not up on their website yet, but I already submitted the proofs. So if you can’t wait — the short article is available here. I admit that it takes a bit of a chutzpah to teach people how to write, so take it as you will.
Like my previous “how to write” article (see also my blog post), this article is mildly opinionated, but hopefully not overly so to remain useful. It is again aimed at a novice writer. There is a major difference between the way fiction is written vs. math, and I am trying to capture it somehow. To give you some flavor, here is a quote:
What kind of a story? Imagine a non-technical and non-detailed version of the abstract of your paper. It should be short, to the point, and straightforward enough to be a tweet, yet interesting enough for one person to want to tell it, and for the listener curious enough to be asking for details. Sounds difficult if not impossible? You are probably thinking that way, because distilled products always lack flavor compared to the real thing. I hear you, but let me give you some examples.
Take Aesop’s fable “The Tortoise and the Hare” written over 2500 years ago. The story would be “A creature born with a gift procrastinated one day, and was overtaken by a very diligent creature born with a severe handicap.” The names of these animals and the manner in which one lost to another are less relevant to the point, so the story is very dry. But there are enough hints to make some readers curious to look up the full story.
Now take “The Terminator”, the original 1984 movie. The story here is (spoiler alert! ) “A man and a machine come from another world to fight in this world over the future of the other world; the man kills the machine but dies at the end.” If you are like me, you probably have many questions about the details, which are in many ways much more exciting than the dry story above. But you see my point – this story is a bit like an extended tag line, yet interesting enough to be discussed even if you know the ending.
It could have been worse! Academic lessons of 2020
Well, this year sure was interesting, and not in a good way. Back in 2015, I wrote a blog post discussing how video talks are here to stay, and how we should all agree to start giving them and embrace watching them, whether we like it or not. I was right about that, I suppose. OTOH, I sort of envisioned a gradual acceptance of this practice, not the shock therapy of a phase transition. So, what happened? It’s time to summarize the lessons and roll out some new predictions.
Note: this post is about the academic life which is undergoing some changes. The changes in real life are much more profound, but are well discussed elsewhere.
Teaching
This was probably the bleakest part of the academic life, much commented upon by the media. Good thing there is more to academia than teaching, no matter what the ignorant critics think. I personally haven’t heard anyone saying post-March 2020, that online education is an improvement. If you are like me, you probably spent much more time preparing and delivering your lectures. The quality probably suffered a little. The students probably didn’t learn as much. Neither party probably enjoyed the experience too much. They also probably cheated quite a bit more. Oh, well…
Let’s count the silver linings. First, it will all be over some time next year. At UCLA, not before the end of Summer. Maybe in the Fall… Second, it could’ve been worse. Much worse. Depending on the year, we would have different issues. Back in 1990, we would all be furloughed for a year living off our savings. In 2000, most families had just one personal computer (and no smartphones, obviously). Let the implications of that sink in. But even in 2010 we would have had giant technical issues teaching on Skype (right?) by pointing our laptop cameras on blackboards with dismal effect. The infrastructure which allows good quality streaming was also not widespread (people were still using Redbox, remember?)
Third, the online technology somewhat mitigated the total disaster of studying in the pandemic time. Students who are stuck in faraway countries or busy with family life can watch stored videos of lectures at their convenience. Educational and grading software allows students to submit homeworks and exams online, and instructors to grade them. Many other small things not worth listing, but worth being thankful for.
Fourth, the accelerated embrace of the educational technology could be a good thing long term, even when things go back to normal. No more emails with scanned late homeworks, no more canceled/moved office hours while away at conferences. This can all help us become better at teaching.
Finally, a long declared “death of MOOCs” is no longer controversial. As a long time (closeted) opponent to online education, I am overjoyed that MOOCs are no longer viewed as a positive experience for university students, more like something to suffer through. Here in CA we learned this awhile ago, as the eagerness of the current Gov. Newsom (back then Lt. Gov.) to embrace online courses did not work out well at all. Back in 2013, he said that the whole UC system needs to embrace online education, pronto: “If this doesn’t wake up the U.C. [..] I don’t know what will.” Well, now you know, Governor! I guess, in 2020, I don’t have to hide my feelings on this anymore…
Research
I always thought that mathematicians can work from anywhere with a good WiFi connection. True, but not really – this year was a mixed experience as lonely introverts largely prospered research wise, while busy family people and extraverts clearly suffered. Some day we will know how much has research suffered in 2020, but for me personally it wasn’t bad at all (see e.g. some of my results described in my previous blog post).
Seminars
I am not even sure we should be using the same word to describe research seminars during the pandemic, as the experience of giving and watching math lectures online are so drastically different compared to what we are used to. Let’s count the differences, which are both positive and negative.
- The personal interactions suffer. Online people are much more shy to interrupt, follow up with questions after the talk, etc. The usual pre- or post-seminar meals allow the speaker to meet the (often junior) colleagues who might be more open to ask questions in an informal setting. This is all bad.
- Being online, the seminar opened to a worldwide audience. This is just terrific as people from remote locations across the globe now have the same access to seminars at leading universities. What arXiv did to math papers, covid did to math seminars.
- Again, being online, the seminars are no longer restricting themselves to local speaks or having to make travel arrangements to out of town speakers. Some UCLA seminars this year had many European speakers, something which would be prohibitively expensive just last year.
- Many seminars are now recorded with videos and slides posted online, like we do at the UCLA Combinatorics and LA Combinatorics and Complexity seminars I am co-organizing. The viewers can watch them later, can fast forward, come back and re-watch them, etc. All the good features of watching videos I extolled back in 2015. This is all good.
- On a minor negative side, the audience is no longer stable as it varies from seminar to seminar, further diminishing personal interactions and making level of the audience somewhat unpredictable and hard to aim for.
- As a seminar organizer, I make it a personal quest to encourage people to turn on their cameras at the seminars by saying hello only to those whose faces I see. When the speaker doesn’t see the faces, whether they are nodding or quizzing, they are clueless whether the they are being clear, being too fast or too slow, etc. Stopping to ask for questions no longer works well, especially if the seminar is being recorded. This invariably leads to worse presentations as the speakers can misjudge the audience reactions.
- Unfortunately, not everyone is capable of handling technology challenges equally well. I have seen remarkably well presented talks, as well as some of extremely poor quality talks. The ability to mute yourself and hide behind your avatar is the only saving grace in such cases.
- Even the true haters of online educations are now at least semi-on-board. Back in May, I wrote to Chris Schaberg dubbed by the insufferable Rebecca Schuman as “vehemently opposed to the practice“. He replied that he is no longer that opposed to teaching online, and that he is now in a “it’s really complicated!” camp. Small miracles…
Conferences
The changes in conferences are largely positive. Unfortunately, some conferences from the Spring and Summer of 2020 were canceled and moved, somewhat optimistically, to 2021. Looking back, they should all have been held in the online format, which opens them to participants from around the world. Let’s count upsides and downsides:
- No need for travel, long time commitments and financial expenses. Some conferences continue charging fees for online participation. This seems weird to me. I realize that some conferences are vehicles to support various research centers and societies. Whatever, this is unsustainable as online conferences will likely survive the pandemic. These organizations should figure out some other income sources or die.
- The conferences are now truly global, so the emphasis is purely on mathematical areas than on the geographic proximity. This suggests that the (until recently) very popular AMS meetings should probably die, making AMS even more of a publisher than it is now. I am especially looking forward to the death of “joint meetings” in January which in my opinion outlived their usefulness as some kind of math extravaganza events bringing everyone together. In fact, Zoom simply can’t bring five thousand people together, just forget about it…
- The conferences are now open to people in other areas. This might seem minor — they were always open. However, given the time/money constraints, a mathematician is likely to go only to conferences in their area. Besides, since they rarely get invited to speak at conferences in other areas, travel to such conferences is even harder to justify. This often leads to groupthink as the same people meet year after year at conferences on narrow subjects. Now that this is no longer an obstacle, we might see more interactions between the fields.
- On a negative side, the best kind of conferences are small informal workshops (think of Oberwolfach, AIM, Banff, etc.), where the lectures are advanced and the interactions are intense. I miss those and hope they come back as they are really irreplaceable in the only setting. If all goes well, these are the only conferences which should definitely survive and even expand in numbers perhaps.
Books and journals
A short summary is that in math, everything should be electronic, instantly downloadable and completely free. Cut off from libraries, thousands of mathematicians were instantly left to the perils of their university library’s electronic subscriptions and their personal book collections. Some fared better than others, in part thanks to the arXiv, non-free journals offering old issues free to download, and some ethically dubious foreign websites.
I have been writing about my copyleft views for a long time (see here, there and most recently there). It gets more and more depressing every time. Just when you think there is some hope, the resilience of paid publishing and reluctance to change by the community is keeping the unfortunate status quo. You would think everyone would be screaming about the lack of access to books/journals, but I guess everyone is busy doing something else. Still, there are some lessons worth noting.
- You really must have all your papers freely available online. Yes, copyrighted or not, the publishers are ok with authors posting their papers on their personal website. They are not ok when others are posting your papers on their websites, so the free access to your papers is on you and your coauthors (if any). Unless you have already done so, do this asap! Yes, this applies even to papers accessible online by subscription to selected libraries. For example, many libraries including all of UC system no longer have access to Elsevier journals. Please help both us and yourself! How hard is it to put the paper on the arXiv or your personal website? If people like Noga Alon and Richard Stanley found time to put hundreds of their papers online, so can you. I make a point of emailing to people asking them to do that every time I come across a reference which I cannot access. They rarely do, and usually just email me the paper. Oh, well, at least I tried…
- Learn to use databases like MathSciNet and Zentralblatt. Maintain your own website by adding the slides, video links as well as all your papers. Make sure to clean up and keep up to date your Google Scholar profile. When left unattended it can get overrun with random papers by other people, random non-research files you authored, separate items for same paper, etc. Deal with all that – it’s easy and takes just a few minutes (also, some people judge them). When people are struggling trying to do research from home, every bit of help counts.
- If you are signing a book contract, be nice to online readers. Make sure you keep the right to display a public copy on your website. We all owe a great deal of gratitude to authors who did this. Here is my favorite, now supplemented with high quality free online lectures. Be like that! Don’t be like one author (who will remain unnamed) who refused to email me a copy of a short 5 page section from his recent book. I wanted to teach the section in my graduate class on posets this Fall. Instead, the author suggested I buy a paper copy. His loss — I ended up teaching some other material instead. Later on, I discovered that the book is already available on one of those ethically compromised websites. He was fighting a battle he already lost!
Home computing
Different people can take different conclusions from 2020, but I don’t think anyone would argue the importance of having good home computing. There is a refreshing variety of ways in which people do this, and it’s unclear to me what is the optimal set up. With a vaccine on the horizon, people might be reluctant to further invest into new computing equipment (or video cameras, lights, whiteboard, etc.), but the holiday break is actually a good time to marinate on what worked out well and what didn’t.
Read your evaluations and take them to heart. Make changes when you see there are problems. I know, it’s unfair, your department might never compensate you for all this stuff. Still, it’s a small price to pay for having a safe academic job in the time of widespread anxiety.
Predictions for the future
- Very briefly: I think online seminars and conferences are here to stay. Local seminars and small workshops will also survive. The enormous AMS meetings and expensive Theory CS meetings will play with the format, but eventually turn online for good or die untimely death.
- Online teaching will remain being offered by every undergraduate math program to reach out to students across the spectrum of personal circumstances. A small minority of courses, but still. Maybe one section of each calculus, linear algebra, intro probability, discrete math, etc. Some faculty might actually prefer this format to stay away from office one semester. Perhaps, in place of a sabbatical, they can ask for permission to spend a semester some other campus, maybe in another state or country, while they continue teaching, holding seminars, supervising students, etc. This could be a perk of academic life to compete with the “remote work” that many businesses are starting to offer on a permanent basis. Universities would have to redefine what they mean by “residence” requirement for both faculty and students.
- More university libraries will play hardball and unsubscribe from major for-profit publishers. This would again sound hopeful, but not gain a snowball effect for at least the next 10 years.
- There will be some standardization of online teaching requirements across the country. Online cheating will remain widespread. Courts will repeatedly rule that business and institutions can discount or completely ignore all 2020 grades as unreliable in large part because of the cheating scandals.
Final recommendations
- Be nice to your junior colleagues. In the winner-take-all no-limits online era, the established and well-known mathematicians get invited over and over, while their junior colleagues get overlooked, just in time when they really need help (job market might be tough this year). So please go out of your way to invite them to give talks at your seminars. Help them with papers and application materials. At least reply to their emails! Yes, even small things count…
- Do more organizing if you are in position to do so. In the absence of physical contact, many people are too shy and shell-shocked to reach out. Seminars, conferences, workshops, etc. make academic life seem somewhat normal and the breaks definitely allow for more interactions. Given the apparent abundance of online events one my be forgiven to think that no more is needed. But more locally focused online events are actually important to help your communities. These can prove critical until everything is back to normal.
Good luck everybody! Hope 2021 will be better for us all!
What if they are all wrong?
Conjectures are a staple of mathematics. They are everywhere, permeating every area, subarea and subsubarea. They are diverse enough to avoid a single general adjective. They come in al shapes and sizes. Some of them are famous, classical, general, important, inspirational, far-reaching, audacious, exiting or popular, while others are speculative, narrow, technical, imprecise, far-fetched, misleading or recreational. That’s a lot of beliefs about unproven claims, yet we persist in dispensing them, inadvertently revealing our experience, intuition and biases.
The conjectures also vary in attitude. Like a finish line ribbon they all appear equally vulnerable to an outsider, but in fact differ widely from race to race. Some are eminently reachable, the only question being who will get there first (think 100 meter dash). Others are barely on the horizon, requiring both great effort, variety of tools, and an extended time commitment (think ironman triathlon). The most celebrated third type are like those Sci-Fi space expeditions in requiring hundreds of years multigenerational commitments, often losing contact with civilization it left behind. And we can’t forget the romantic fourth type — like the North Star, no one actually wants to reach them, as they are largely used for navigation, to find a direction in unchartered waters.
Now, conjectures famously provide a foundation of the scientific method, but that’s not at all how we actually think of them in mathematics. I argued back in this pointed blog post that citations are the most crucial for the day to day math development, so one should take utmost care in making references. While this claim is largely uncontroversial and serves as a raison d’être for most GoogleScholar profiles, conjectures provide a convenient idealistic way out. Thus, it’s much more noble and virtuous to say “I dedicated my life to the study of the XYZ Conjecture” (even if they never publish anything), than “I am working hard writing so many papers to gain respect of my peers, get a promotion, and provide for my family“. Right. Obviously…
But given this apparent (true or perceived) importance of conjectures, are you sure you are using them right? What if some/many of these conjectures are actually wrong, what then? Should you be flying that starship if there is no there there? An idealist would argue something like “it’s a journey, not a destination“, but I strongly disagree. Getting closer to the truth is actually kind of important, both as a public policy and on an individual level. It is thus pretty important to get it right where we are going.
What are conjectures in mathematics?
That’s a stupid question, right? Conjectures are mathematical claims whose validity we are trying to ascertain. Is that all? Well, yes, if you don’t care if anyone will actually work on the conjecture. In other words, something about the conjecture needs to interesting and inspiring.
What makes a conjecture interesting?
This is a hard question to answer because it is as much psychological as it is mathematical. A typical answer would be “oh, because it’s old/famous/beautiful/etc.” Uhm, ok, but let’s try to be a little more formal.
One typically argues “oh, that’s because this conjecture would imply [a list of interesting claims and known results]”. Well, ok, but this is self-referential. We already know all those “known results”, so no need to prove them again. And these “claims” are simply other conjectures, so this is really an argument of the type “this conjecture would imply that conjecture”, so not universally convincing. One can argue: “look, this conjecture has so many interesting consequences”. But this is both subjective and unintuitive. Shouldn’t having so many interesting conjectural consequences suggest that perhaps the conjecture is too strong and likely false? And if the conjecture is likely to be false, shouldn’t this make it uninteresting?
Also, wouldn’t it be interesting if you disprove a conjecture everyone believes to be true? In some sense, wouldn’t it be even more interesting if until now everyone one was simply wrong?
None of this are new ideas, of course. For example, faced with the need to justify the “great” BC conjecture, or rather 123 pages of survey on the subject (which is quite interesting and doesn’t really need to be justified), the authors suddenly turned reflective. Mindful of self-referential approach which they quickly discard, they chose a different tactic:
We believe that the interest of a conjecture lies in the feeling of unity of mathematics that it entails. [M.P. Gomez Aparicio, P. Julg and A. Valette, “The Baum-Connes conjecture“, 2019]
Huh? Shouldn’t math be about absolute truths, not feelings? Also, in my previous blog post, I mentioned Noga Alon‘s quote that Mathematics is already “one unit“. If it is, why does it need a new “feeling of unity“? Or is that like one of those new age ideas which stop being true if you don’t reinforce them at every occasion?
If you are confused at this point, welcome to the club! There is no objective way to argue what makes certain conjectures interesting. It’s all in our imagination. Nikolay Konstantinov once told me that “mathematics is a boring subject because every statement is equivalent to saying that some set is empty.” He meant to be provocative rather than uninspiring. But the problem he is underlying is quite serious.
What makes us believe a conjecture is true?
We already established that in order to argue that a conjecture is interesting we need to argue it’s also true, or at least we want to believe it to be true to have all those consequences. Note, however, that we argue that a conjecture is true in exactly the same way we argue it’s interesting: by showing that it holds is some special cases, and that it would imply other conjectures which are believed to be true because they are also checked in various special cases. So in essence, this gives “true = interesting” in most cases. Right?
This is where it gets complicated. Say, you are working on the “abc conjecture” which may or may not be open. You claim that it has many consequences, which makes it both likely true and interesting. One of them is the negative solution to the Erdős–Ulam problem about existence of a dense set in the plane with rational pairwise distances. But a positive solution to the E-U problem implies the Harborth’s conjecture (aka the “integral Fáry problem“) that every graph can be drawn in the plane with rational edge lengths. So, counterintuitively, if you follow the logic above shouldn’t you be working on a positive solution to Erdős–Ulam since it would both imply one conjecture and give a counterexample to another? For the record, I wouldn’t do that, just making a polemical point.
I am really hoping you see where I am going. Since there is no objective way to tell if a conjecture is true or not, and what exactly is so interesting about it, shouldn’t we discard our biases and also work towards disproving the conjecture just as hard as trying to prove it?
What do people say?
It’s worth starting with a general (if slightly poetic) modern description:
In mathematics, [..] great conjectures [are] sharply formulated statements that are most likely true but for which no conclusive proof has yet been found. These conjectures have deep roots and wide ramifications. The search for their solution guides a large part of mathematics. Eternal fame awaits those who conquer them first. Remarkably, mathematics has elevated the formulation of a conjecture into high art. [..] A well-chosen but unproven statement can make its author world-famous, sometimes even more so than the person providing the ultimate proof. [Robbert Dijkgraaf, The Subtle Art of the Mathematical Conjecture, 2019]
Karl Popper thought that conjectures are foundational to science, even if somewhat idealized the efforts to disprove them:
[Great scientists] are men of bold ideas, but highly critical of their own ideas: they try to find whether their ideas are right by trying first to find whether they are not perhaps wrong. They work with bold conjectures and severe attempts at refuting their own conjectures. [Karl Popper, Heroic Science, 1974]
Here is how he reconciled somewhat the apparent contradiction:
On the pre-scientific level we hate the very idea that we may be mistaken. So we cling dogmatically to our conjectures, as long as possible. On the scientific level, we systematically search for our mistakes. [Karl Popper, quoted by Bryan Magee, 1971]
Paul Erdős was, of course, a champion of conjectures and open problems. He joked that the purpose of life is “proof and conjecture” and this theme is repeatedly echoed when people write about him. It is hard to overestimate his output, which included hundreds of talks titled “My favorite problems“. He wrote over 180 papers with collections of conjectures and open problems (nicely assembled by Zbl. Math.)
Peter Sarnak has a somewhat opposite point of view, as he believes one should be extremely cautious about stating a conjecture so people don’t waste time working on it. He said once, only half-jokingly:
Since we reward people for making a right conjecture, maybe we should punish those who make a wrong conjecture. Say, cut off their fingers. [Peter Sarnak, UCLA, c. 2012]
This is not an exact quote — I am paraphrasing from memory. Needless to say, I disagree. I don’t know how many fingers he wished Erdős should lose, since some of his conjectures were definitely disproved: one, two, three, four, five, and six. This is not me gloating, the opposite in fact. When you are stating hundreds of conjectures in the span of almost 50 years, having only a handful to be disproved is an amazing batting average. It would, however, make me happy if Sarnak’s conjecture is disproved someday.
Finally, there is a bit of a controversy whether conjectures are worth as much as theorems. This is aptly summarized in this quote about yet another champion of conjectures:
Louis J. Mordell [in his book review] questioned Hardy‘s assessment that Ramanujan was a man whose native talent was equal to that of Euler or Jacobi. Mordell [..] claims that one should judge a mathematician by what he has actually done, by which Mordell seems to mean, the theorems he has proved. Mordell’s assessment seems quite wrong to me. I think that a felicitous but unproved conjecture may be of much more consequence for mathematics than the proof of many a respectable theorem. [Atle Selberg, “Reflections Around the Ramanujan Centenary“, 1988]
So, what’s the problem?
Well, the way I see it, the efforts made towards proving vs. disproving conjectures is greatly out of balance. Despite all the high-minded Popper’s claims about “severe attempts at refuting their own conjectures“, I don’t think there is much truth to that in modern math sciences. This does not mean that disproofs of famous conjectures aren’t celebrated. Sometimes they are, see below. But it’s clear to me that the proofs are celebrated more frequently, and to a much greater degree. I have only anecdotal evidence to support my claim, but bear with me.
Take prizes. Famously, Clay Math Institute gives $1 million for a solution of any of these major open problems. But look closely at the rules. According to the item 5b, except for the P vs. NP problem and the Navier–Stokes Equation problem, it gives nothing ($0) for a disproof of these problems. Why, oh why?? Let’s look into CMI’s “primary objectives and purposes“:
To recognize extraordinary achievements and advances in mathematical research.
So it sounds like CMI does not think that disproving the Riemann Hypothesis needs to be rewarded because this wouldn’t “advance mathematical research”. Surely, you are joking? Whatever happened to “the opposite of a profound truth may well be another profound truth“? Why does the CMI wants to put its thumb on the scale and support only one side? Do they not want to find out the solution whatever it is? Shouldn’t they be eager to dispense with the “wrong conjecture” so as to save numerous researches from “advances to nowhere“?
I am sure you can see that my blood is boiling, but let’s proceed to the P vs. NP problem. What if it’s independent of ZFC? Clearly, CMI wouldn’t pay for proving that. Why not? It’s not like this kind of thing never happened before (see obligatory link to CH). Some people believe that (or at least they did in 2012), and some people like Scott Aaronson take this seriously enough. Wouldn’t this be a great result worthy of an award as much as the proof that P=NP, or at least a nonconstructive proof that P=NP?
If your head is not spinning hard enough, here is another amusing quote:
Of course, it’s possible that P vs. NP is unprovable, but that that fact itself will forever elude proof: indeed, maybe the question of the independence of P vs. NP is itself independent of set theory, and so on ad infinitum! But one can at least say that, if P vs. NP (or for that matter, the Riemann hypothesis, Goldbach’s conjecture, etc.) were proven independent of ZF, it would be an unprecedented development. [Scott Aaronson, P vs. NP, 2016].
Speaking of Goldbach’s Conjecture, the most talked about and the most intuitively correct statement in Number Theory that I know. In a publicity stunt, for two years there was a $1 million prize by a publishing house for the proof of the conjecture. Why just for the proof? I never heard of anyone not believing the conjecture. If I was the insurance underwriter for the prize (I bet they had one), I would allow them to use “for the proof or disproof” for a mere extra $100 in premium. For another $50 I would let them use “or independent of ZF” — it’s a free money, so why not? It’s such a pernicious idea of rewarding only one kind of research outcome!
Curiously, even for Goldbach’s Conjecture, there is a mild divergence of POVs on what the future holds. For example, Popper writes (twice in the same book!) that:
[On whether Goldbach’s Conjecture is ‘demonstrable’] We don’t know: perhaps we may never know, and perhaps we can never know. [Karl Popper, Conjectures and Refutations, 1963]
Ugh. Perhaps. I suppose anything can happen… For example, our civilizations can “perhaps” die out in the next 200 years. But is that likely? Shouldn’t the gloomy past be a warning, not a prediction of the future? The only thing more outrageously pessimistic is this theological gem of a quote:
Not even God knows the number of permutations of 1000 avoiding the 1324 pattern. [Doron Zeilberger, quoted here, 2005]
Thanks, Doron! What a way to encourage everyone! Since we know from numerical estimates that this number is ≈ 3.7 × 101017 (see this paper and this follow up), Zeilberger is suggesting that large pattern avoidance numbers are impossibly hard to compute precisely, already in the range of only about 1018 digits. I really hope he is proved wrong in his lifetime.
But I digress. What I mean to emphasize, is that there are many ways a problem can be resolved. Yet some outcomes are considered more valuable than others. Shouldn’t the research achievements be rewarded, not the desired outcome? Here is yet another colorful opinion on this:
Given a conjecture, the best thing is to prove it. The second best thing is to disprove it. The third best thing is to prove that it is not possible to disprove it, since it will tell you not to waste your time trying to disprove it. That’s what Gödel did for the Continuum Hypothesis. [Saharon Shelah, Rutgers Univ. Colloqium, 2001]
Why do I care?
For one thing, disproving conjectures is part of what I do. Sometimes people are a little shy to unambiguously state them as formal conjectures, so they phrase them as questions or open problems, but then clarify that they believe the answer is positive. This is a distinction without a difference, or at least I don’t see any (maybe they are afraid of Sarnak’s wrath?) Regardless, proving their beliefs wrong is still what I do.
For example, here is my old bog post on my disproof of the Noonan-Zeiberger Conjecture (joint with Scott Garrabrant). And in this recent paper (joint with Danny Nguyen), we disprove in one big swoosh both Barvinok’s Problem, Kannan’s Problem, and Woods Conjecture. Just this year I disproved three conjectures:
- The Kirillov–Klyachko Conjecture (2004) that the reduced Kronecker coefficients satisfy the saturation property (this paper, joint with Greta Panova).
- The Brandolini et al. Conjecture (2019) that concrete lattice polytopes can multitile the space (this paper, joint with Alexey Garber).
- Kenyon’s Problem (c. 2005) that every integral curve in R3 is a boundary of a PL surface comprised of unit triangles (this paper, joint with Alexey Glazyrin).
On top of that, just two months ago in this paper (joint with Han Lyu), we showed that the remarkable independence heuristic by I. J. Good for the number of contingency tables, fails badly even for nearly all uniform marginals. This is not exactly disproof of a conjecture, but it’s close, since the heuristic was introduced back in 1950 and continues to work well in practice.
In addition, I am currently working on disproving two more old conjectures which will remain unnamed until the time we actually resolve them (which might never happen, of course). In summary, I am deeply vested in disproving conjectures. The reasons why are somewhat complicated (see some of them below). But whatever my reasons, I demand and naively fully expect that my disproofs be treated on par with proofs, regardless whether this expectation bears any relation to reality.
My favorite disproofs and counterexamples:
There are many. Here are just a few, some famous and some not-so-famous, in historical order:
- Fermat‘s conjecture (letter to Pascal, 1640) on primality of Fermat numbers, disproved by Euler (1747)
- Tait’s conjecture (1884) on hamiltonicity of graphs of simple 3-polytopes, disproved by W.T. Tutte (1946)
- General Burnside Problem (1902) on finiteness of periodic groups, resolved negatively by E.S. Golod (1964)
- Keller’s conjecture (1930) on tilings with unit hypercubes, disproved by Jeff Lagarias and Peter Shor (1992)
- Borsuk’s Conjecture (1932) on partitions of convex sets into parts of smaller diameter, disproved by Jeff Kahn and Gil Kalai (1993)
- Hirsch Conjecture (1957) on the diameter of graphs of convex polytopes, disproved by Paco Santos (2010)
- Woods’s conjecture (1972) on the covering radius of certain lattices, disproved by Oded Regev, Uri Shapira and Barak Weiss (2017)
- Connes embedding problem (1976), resolved negatively by Zhengfeng Ji, Anand Natarajan, Thomas Vidick, John Wright and Henry Yuen (2020)
In all these cases, the disproofs and counterexamples didn’t stop the research. On the contrary, they gave a push to further (sometimes numerous) developments in the area.
Why should you disprove conjectures?
There are three reasons, of different nature and importance.
First, disproving conjectures is opportunistic. As mentioned above, people seem to try proving much harder than they try disproving. This creates niches of opportunity for an open-minded mathematician.
Second, disproving conjectures is beautiful. Let me explain. Conjectures tend to be rigid, as in “objects of the type pqr satisfy property abc.” People like me believe in the idea of “universality“. Some might call it “completeness” or even “Murphy’s law“, but the general principle is always the same. Namely: it is not sufficient that one wishes that all pqr satisfy abc to actually believe in the implication; rather, there has to be a strong reason why abc should hold. Barring that, pqr can possibly be almost anything, so in particular non-abc. While some would argue that non-abc objects are “ugly” or at least “not as nice” as abc, the idea of universality means that your objects can be of every color of the rainbow — nice color, ugly color, startling color, quiet color, etc. That kind of palette has its own sense of beauty, but it’s an acquired taste I suppose.
Third, disproving conjectures is constructive. It depends on the nature of the conjecture, of course, but one is often faced with necessity to construct a counterexample. Think of this as an engineering problem of building some pqr which at the same time is not abc. Such construction, if at all possible, might be difficult, time consuming and computer assisted. But so what? What would you rather do: build a mile-high skyscraper (none exist yet) or prove that this is impossible? Curiously, in CS Theory both algorithms and (many) complexity results are constructive (you need gadgets). Even the GCT is partially constructive, although explaining that would take us awhile.
What should the institutions do?
If you are an institution which awards prizes, stop with the legal nonsense: “We award […] only for a publication of a proof in a top journal”. You need to set up a scientific committee anyway, since otherwise it’s hard to tell sometimes if someone deserves a prize. With mathematicians you can expect anything anyway. Some would post two arXiv preprints, give a few lectures and then stop answering emails. Others would publish only in a journal where they are Editor-in-Chief. It’s stranger than fiction, really.
What you should do is say in the official rules: “We have [this much money] and an independent scientific committee which will award any progress on [this problem] partially or in full as they see fit.” Then a disproof or an independence result will receive just as much as the proof (what’s done is done, what else are you going to do with the money?) This would also allow some flexibility for partial solutions. Say, somebody proves Goldbach’s Conjecture for integers > exp(exp(10100000)), way way beyond computational powers for the remaining integers to be checked. I would give this person at least 50% of the prize money, leaving the rest for future developments of possibly many people improving on the bound. However, under the old prize rules such person gets bupkes for their breakthrough.
What should the journals do?
In short, become more open to results of computational and experimental nature. If this sounds familiar, that’s because it’s a summary of Zeilberger’s Opinions, viewed charitably. He is correct on this. This includes publishing results of the type “Based on computational evidence we believe in the following UVW conjecture” or “We develop a new algorithm which confirms the UVW conjecture for n<13″. These are still contributions to mathematics, and the journals should learn to recognize them as such.
To put in context of our theme, it is clear that a lot more effort has been placed on proofs than on finding counterexamples. However, in many areas of mathematics there are no small counterexamples, so a heavy computational effort is crucial for any hope of finding one. Such work is not be as glamorous as traditional papers. But really, when it comes to standards, if a journal is willing to publish the study of something like the “null graphs“, the ship has sailed for you…
Let me give you a concrete example where a computational effort is indispensable. The curious Lovász conjecture states that every finite connected vertex-transitive graph contains a Hamiltonian path. This conjecture got to be false. It hits every red flag — there is really no reason why pqr = “vertex transitive” should imply abc = “Hamiltonian”. The best lower bound for the length of the longest (self-avoiding) path is only about square root of the number of vertices. In fact, even the original wording by Lovász shows he didn’t believe the conjecture is true (also, I asked him and he confirmed).
Unfortunately, proving that some potential counterexample is not Hamiltonian is computationally difficult. I once had an idea of one (a nice cubic Cayley graph on “only” 3600 vertices), but Bill Cook quickly found a Hamiltonian cycle dashing my hopes (it was kind of him to look into this problem). Maybe someday, when the TSP solvers are fast enough on much larger graphs, it will be time to return to this problem and thoroughly test it on large Cayley graphs. But say, despite long odds, I succeed and find a counterexample. Would a top journal publish such a paper?
Editor’s dilemma
There are three real criteria for evaluation a solution of an open problem by the journal:
- Is this an old, famous, or well-studied problem?
- Are the tools interesting or innovative enough to be helpful in future studies?
- Are the implications of the solution to other problems important enough?
Now let’s make a hypothetical experiment. Let’s say a paper is submitted to a top math journal which solves a famous open problem in Combinatorics. Further, let’s say somebody already proved it is equivalent to a major problem in TCS. This checks criteria 1 and 3. Until not long ago it would be rejected regardless, so let’s assume this is happening relatively recently.
Now imagine two parallel worlds, where in the first world the conjecture is proved on 2 pages using beautiful but elementary linear algebra, and in the second world the conjecture is disproved on a 2 page long summary of a detailed computational search. So in neither world we have much to satisfy criterion 2. Now, a quiz: in which world the paper will be published?
If you recognized that the first world is a story of Hao Huang‘s elegant proof of the induced subgraphs of hypercubes conjecture, which implies the sensitivity conjecture. The Annals published it, I am happy to learn, in a welcome break with the past. But unless we are talking about some 200 year old famous conjecture, I can’t imagine the Annals accepting a short computational paper in the second world. Indeed, it took a bit of a scandal to accept even the 400 year old Kepler’s conjecture which was proved in a remarkable computational work.
Now think about this. Is any of that fair? Shouldn’t we do better as a community on this issue?
What do other people do?
Over the years I asked a number of people about the uncertainty created by the conjectures and what do they do about it. The answers surprised me. Here I am paraphrasing them:
Some were dumbfounded: “What do you mean this conjecture could be false? It has to be true, otherwise nothing I am doing make much sense.”
Others were simplistic: “It’s an important conjecture. Famous people said it’s true. It’s my job to prove it.”
Third were defensive: “Do you really think this conjecture could be wrong? Why don’t you try to disprove it then? We’ll see who is right.”
Fourth were biblical: “I tend to work 6 days a week towards the proof and one day towards the disproof.”
Fifth were practical: “I work on the proof until I hit a wall. I use the idea of this obstacle to try constructing potential counterexamples. When I find an approach to discard such counterexamples, I try to generalize the approach to continue working on the proof. Continue until either side wins.”
If the last two seem sensible to you to, that’s because they are. However, I bet fourth are just grandstanding — no way they actually do that. The fifth sound great when this is possible, but that’s exceedingly rare, in my opinion. We live in a technical age when proving new results often requires great deal of effort and technology. You likely have tools and intuition to work in only one direction. Why would you want to waste time working in another?
What should you do?
First, remember to make conjectures. Every time you write a paper, tell a story of what you proved. Then tell a story of what you wanted to prove but couldn’t. State it in the form of a conjecture. Don’t be afraid to be wrong, or be right but oversharing your ideas. It’s a downside, sure. But the upside is that your conjecture might prove very useful to others, especially young researchers. In might advance the area, or help you find a collaborator to resolve it.
Second, learn to check your conjectures computationally in many small cases. It’s important to give supporting evidence so that others take your conjectures seriously.
Third, learn to make experiments, explore the area computationally. That’s how you make new conjectures.
Fourth, understand yourself. Your skill, your tools. Your abilities like problem solving, absorbing information from the literature, or making bridges to other fields. Faced with a conjecture, use this knowledge to understand whether at least in principle you might be able to prove or disprove a conjecture.
Fifth, actively look for collaborators. Those who have skills, tools, or abilities you are missing. More importantly, they might have a different POV on the validity of the conjecture and how one might want to attack it. Argue with them and learn from them.
Sixth, be brave and optimistic! Whether you decide to prove, disprove a conjecture, or simply state a new conjecture, go for it! Ignore the judgements by the likes of Sarnak and Zeilberger. Trust me — they don’t really mean it.
The guest publishing scam
For years, I have been a staunch opponent of “special issues” which proliferate many good journals. As an editor, when asked by the publisher if we should have some particular guest issue I would always say no, only to be outvoted or overruled by the Editor in Chief. While I always believed there is some kind of scam going on, I never really thought about it. In fact, it’s really on the surface for everyone to see…
What is so special about special issues?
Well, let me explain how this works. Imagine you organized an annual conference and you feel it was a success. Or you organized a birthday/memorial conference in honor of a senior colleague in the area and want to do more. You submit a proposal to a journal: please, please, can we become “guest editors” and publish a “special issue” of the journal? Look, our conference had so many terrific people, and the person we are honoring is such a great mathematician, so famous and so kind to everyone, how can you say no?
And the editors/publishers do say yes. Not always. Sometimes. If one journal refuses, the request is made to another journal. Eventually, like with paper submissions, some journal says “sure”. The new guest editors quickly ask all/some conference speakers to submit papers. Some/many do. Most of these papers get accepted. Not a rule, just social contract. As in “how dare you reject this little paper by a favorite student of the honoree?”
The journal publishes them with an introductory article by guest editors lauding the conference. A biographical article with reminiscences is also included, with multiple pictures from earlier conferences or from the family archive, always showing light side of the great person. The paper version of the journal is then sent to all authors, or is presented with a pomp to the honoree at some retirement party as some kind of math version of a gold watch. None of them will ever open the volume. These issues will be recycled at best, as everyone will continue to use online versions.
Sounds like a harmless effort, don’t you see? Nobody is acting dishonorably, and mathematicians get to publish more papers, journals get to have submissions the wouldn’t otherwise, the conference or a person gets honored. So, win-win-win, right? Well, hear me out.
Why do the journal editors do it?
We leave the publishers for last. For a journal editor in chief this is straightforward. If they work for leading for-profit publishers they get paid. For a good reason in fact — it’s a hard work. Now, say some friends ask to do part of your job for free, and the proposal looks good, and the list of potential authors is pretty reasonable perhaps. You get to help yourself, your friends, and the area you favor, without anyone ever holding you responsible for the outcome. Low level corruption issues set aside and ignored, who wouldn’t take this deal?
Why do the guest editors do it?
Well, this is the easiest question. Some want to promote the area, some to honor the honoree, some just want to pad their CVs. It’s all good as far as I am concerned. They are not the problem.
Why do the authors do it?
Well, for multiple reasons. Here are some possible scenarios based on my observations. Some are honorable, some are dishonorable, and some in between.
Some authors care deeply for the subject or the honoree. They send their best work to the invited issue. This is their way to give back. Most likely they could’ve published that paper in a much better journal. Nobody will ever appreciate their “sacrifice”, but they often don’t care, it makes them feel better, and they have a really good excuse anyway. From the journal POV these are the best papers. Grade A.
Other authors think of these special issues completely differently and tailor make the paper to the issue. For example, they write personal memoir style reminiscences, as in “ideas from my conversations with X”, or “the influence of X on my work”. Other times they write nice surveys, as in “how X’s work changed field ABC”, or “recent progress on X’s conjectures”. The former are usually low on math content but mildly entertaining, even if not always appropriate for a traditional math journal (but why be constrained with old conventions?) The latter can be quite useful in a way surveys are often in demand, even if the timing for these particular surveys can be a little forced. Also, both are quite appropriate for these specific issues. Anyway, Grade B.
Some authors are famous, write many papers a year, have published in all good and even not-so-good journals multiple times already, so they don’t care which journal they submit next. Somebody asks them to honor somebody/something, and they want to be nice and send their next paper whether or not it’s good or bad, or even remotely related to the subject. And why not? Their name on the paper is what matters anyway, right? Or at least that’s what they think. Grade C.
Some authors have problematic papers which they desperately want to publish. Look, doing research, writing papers and publishing is hard, I get it. Sometimes you aim to prove a big deal and just almost nothing comes out, but you still want to report on your findings just as a tribute to the time you spent on the problem. Or a paper was rejected from a couple of journals and you are close to typing up a stronger result, so want to find a home for the paper asap before it becomes unpublishable at your own hand! Or you haven’t published for years, you’re worried your department may refuse you a promotion, so you want to publish anything, anywhere, just to get a new line on your CV. So given a chance you submit, with an understanding that whatever you submit will likely get published. The temptation is just too strong to look away. I don’t approve, if you can’t tell… Grade D/F.
Why do the publishers do it?
That’s where the scam is. Let me give you a short version before you quit reading, and expound on it below. Roughly — publisher’s contracts with libraries require them to deliver a certain number of pages each year. But the editorial boards are somewhat unruly, unpredictable and partly dysfunctional, like many math departments I suppose. Sometimes they over-accept papers by creating large backlogs and lowering standards. Other times, they are on a quest to raise standards and start to reject a lot of submissions. The journals are skittish about increasing and especially about decreasing the page numbers which would lead to their loss of income, creating a desperate need for more pages, any pages they can publish and mail to the libraries. This vacuum is then happily filled with all those special issues.
What made me so upset that I decided to blog on this?
Look, there is always something that’s a last drop. In this case it was a reference to my paper, and not a good kind. At some point Google Scholar informed me about a paper with a curious title citing a rather technical paper of mine. So I clicked. Here is the citation, in its full glory:
“Therefore, people need to think about the principles and methods of knowledge storage, management and application from a new perspective, and transform human knowledge into a form that can be understood and applied by machines at a higher level—the knowledge map, which is realized on the basis of information interconnection to change knowledge interconnection possible [27].”
Visualization Analysis of Knowledge Network Research Based on Mapping Knowledge, by Hong Liu, Ying Jiang, Hua Fan, Xin Wang & Kang Zhao, Journal of Signal Processing Systems (2020)
And here is [27]: Pak, I., & Panova, G. (2017). On the complexity of computing Kronecker coefficients, Computational Complexity, 26, 1–36.
Now, I reread the above quote three times and understood nothing. Naturally, I know my paper [27] rather well. It is a technical result on computational complexity of computing certain numbers which naturally arise in Algebraic Combinatorics, and our approach uses symmetric functions, Young tableau combinatorics and Barvinok’s algorithm. We definitely say nothing about the “knowledge storage” or “interconnection” or “management” of any of that.
Confused, I let it go, but an unrelated Google search brought up the paper again. So I reread the quote three more times. Finally convinced this is pure nonsense, I googled the journal to see if it’s one of the numerous spam journals I hear about.
Turns out, the Journal of Signal Processing Systems (JSPS) is a serious journal in the area, with impact factor around 1, and H-index of 49. For comparison, the European Journal of Combinatorics has impact factor around 0.9 and H-index of 45.
Now, JSPS has three main editors — Sun-Yuan Kung from Princeton, Shuvra S. Bhattacharyya from University of Maryland College Park, and Jarmo Takala from Tampere University in Helsinki. All reputable people. For example, Kung has over 30K citations on Google Scholar, while Takala has over 400 published papers.
So, in my usual shy and unassuming way, I wrote to them a short email on Sep 25, 2020, inquiring about the fateful citation:
Dear Editors,
I want to bring to your attention the following article recently published in the Journal of Signal Processing Systems. I personally have neither knowledge nor expertise in your field, so I can’t tell you whether this is indeed a spam article. However, I can tell when I see a bogus citation to my own work, which is used to justify some empty verbosity. Please do keep me posted as to what actions you intend to take on the matter (if any).
Best, — Igor Pak
Here is the reply that I got:
Dear Prof. Pak,
thank you for providing feedback about the citation in this article. The article is published in a special issue, where the papers have been selected by guest editors. We will have a discussion with the guest editors on this matter. Sincerely,
Jarmo Takala
Co-Editor-inChief J. Signal Processing Systems
Now you see what I mean? It’s been over a month since my email. The paper is still there. Clearly going nowhere. The editors basically take no responsibility as they did not oversee the guest issue. They have every incentive to blame someone else and drop the discussion, because this whole thing can only lead to embarrassment and bad rep. This trick is called “blame shifting”.
Meanwhile, the guest editors have no incentives to actually do anything because they are not affiliated with the journal. In fact, you can’t even tell from the Editors’ email or from the paper who they are. So I still don’t know who they are and have no way to reach out to them. The three Editors above never replied to my later email, so I guess we are stuck. All right then, maybe the time will tell….
Explaining the trick in basic terms
I am not sure what the business term for this type of predatory behavior, but let me give you some familiar examples so you get the idea.
(1) Say, you are a large very old liberal arts university located in Cambridge, MA. Yes, like Harvard. Almost exactly like Harvard. You have a fancy very expensive college with very low admission rate of less than 1 in 20. But you know you are a good brand, and every time you make some rich kid go away, your treasurer’s heart is bleeding. So how do you make more money off the brand?
Well, you start an Extension School which even gives Bachelor and Master’s degrees. And it’s a moneymaker! It brings over $500 million each year, about the same as the undergraduate and graduate tuitions combined! But wait, careful! You do give them “Harvard degrees“, just not “Harvard College degrees“. And, naturally, they would never include the Extension School students in the “average SAT score” or “income one year after graduation” stats they report to US News, because it’s not Harvard College, don’t you understand?
Occasionally this leads to confusion and even minor scandals, but who cares, right? We are talking a lot of money! A lot of people have afterhours adjunct jobs, rooms have higher occupancy rate aiming to recoup building repairs (well, pre-pandemic), and a lot of people get educated and feel good about getting an education at Harvard, win-win-win…
But you see where I am going — same brand is split into two under one roof, selling two different, highly unequal, almost unrelated products, all for the benefit of a very rich private corporation.
(2) Now, here is a sweet completely made up example. You are a large corporation selling luxury dark chocolate candies made of very expensive cocoa beans. A new CEO comes up with a request. Cut candy weight to save on the beans without lowering candy box prices, and make it a PR campaign so that everyone feels great and rushes to buy these. You say impossible? Not at all!
Here is what you do. Say, your luxury box of dark chocolate candies weights 200 grams, so each is 20 grams. You make each candy a little bit smaller, so the total weight is now 175 gram — for each candy the difference of 2.5 grams is barely noticeable. You make the candy box bigger and put two more rather large 25 gram candies made out of cheap white chocolate, wrapped into a visually different wrap. You sell them in one box. The new weight is 225 grams, i.e. larger than before. You advertise “now with two bonus candies at the same price!”, and customers feel happy to get some “free stuff”. At the end, they might not like the cheap candies, but who cares – they get to have the same old 10 expensive candies, right?
Again, you see where I am going. They created an artificial confusion by selling a superior and an inferior product in the same box without an honest breakdown, so the customers are completely duped.
Back to publishers
They are playing just as unfair as the second example above. The librarians can’t tell the difference between quality of “special issues”, they only negotiate on the number of pages. The journal’s reputation doesn’t suffer from those. Indeed, it is understood that they are not always but often enough of lower quality, but you can’t really submit there unless you are in the loop. I don’t know how the impact factor and H index are calculated, but I bet the publishers work with Web Of Science to exclude these special issues and report only the usual issues akin to the Harvard example. Or not. Nobody cares for these indices anymore, right?
Some examples
Let me just show how chaotic is the publishing of special issues. Take Discrete Mathematics, an Elsevier journal where I was an editor for 8 years (and whose Wikipedia page I made myself). Here is a page with Special Issues. There is no order to any of these conferences. There are 8th French Combinatorial Conference, Seventh Czech-Slovak International Symposium, 23rd British Combinatorics Conference, huh? What happened to the previous 7, 6 and 22 proceedings, respectively? You notice a lot of special issues from before the journal was overhauled and very few in recent years. Clearly the journal is on the right track. Good for them!
Here are three special issues in JCTA, and here are two in JCTB (both Elsevier). Why these? Are the editors sure these have the same quality as the rest of these top rated journals? Well, hopefully no longer top rated for JCTA. The Annals of Combinatorics (Springer) has literally “Ten Years of BAD Math” special issue (yes, I know what BAD Math means, but the name is awful even if the papers are great). The European Journal of Combinatorics (Elsevier again), publishes usually 1-2 special issue per year. Why?? Not enough submissions? Same for Advances Applied Math (also Elsevier), although very few special issues in recent years (good!). I think one of my papers (of grade B) is in one of the older special issues. Ooops!
Now compare these with the Electronic Journal of Combinatorics which stopped publishing special issues back in 2012. This journal is free online, has no page limitation, so it cares more about its reputation than filling the pages. Or take the extreme case of the Annals of Mathematics which would laugh at the idea of a “special issue”. Now you get it!
What gives?
It’s simple, really. STOP publishing special issues! If you are an Editor in Chief, just refuse! Who really knows what kind of scam the guest editors or the publishers are running? But you know your journal, all papers go through you, and you are responsible for all accepted papers. Really, the journal editors are the only ones responsible for journal reputation and for the peer review!
Expensive for profit publishers enjoying side special issue scam — I’ve been looking forward to your demise for a long while. Even more recently I felt optimistic since a lot of papers are now freely accessible. Now that we are all cut off from the libraries during pandemic — can we all agree that these publishers bring virtually no added value??
If you are a potential guest editor who really wants to organize a special issue based on your conference, or to honor somebody, ask publishers to make a special book deal. They might. They do it all the time, even if this is a bit less lucrative business than journal publishing. Individual mathematicians don’t, but the libraries do buy these volumes. And they should.
If you are a potential contributor to a special issue — do what is listed above in Grade B (write a special topic survey or personal reminiscences), which will be published in a book as a chapter. No serious peer review research. These go to journals.
And if you are one of those scam journal publishers who keep emailing me every week to become a special issue editor because you are so enthralled with my latest arXiv preprint — you go die in a ditch!
Final Disclaimer: All these bad opinions are not at all about any particular journal or special issue. There are numerous good papers published in special issues, and these issues are often dedicated to just wonderful mathematicians. I myself admit of publishing papers in a several such special issues. Here I am making a general point which is hopefully clear.
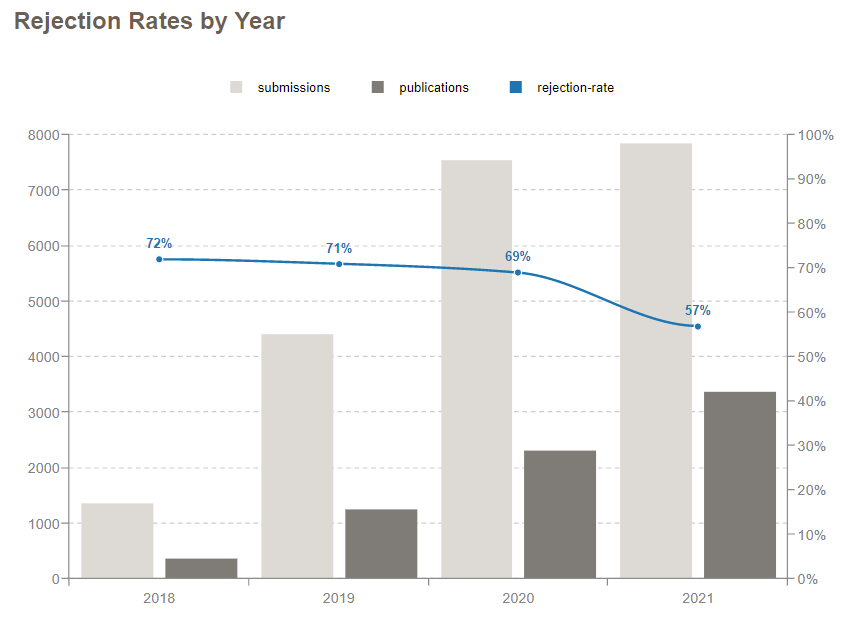

You must be logged in to post a comment.